|
Question 1172342: How many squares on the co-ordinate plane exist with one vertex at P(-1,1) and having atleast one of the coordinate axes as axis of symmetry...??
Found 2 solutions by greenestamps, math_tutor2020:
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The four axes of symmetry of a square are the two lines joining midpoints of opposite sides and the two diagonals.
If one of the coordinate axes is an axis of symmetry of the square, then the square has its sides either parallel to the coordinate axes, or at 45 degree angles to them.
If a square has its sides parallel to the coordinate axes and one vertex of the square is at (-1,1) then the side length of the square must be 2. There are four squares with side length 2, sides parallel to the coordinate axes, and one vertex at (-1,1). How many of them have at least one of the coordinate axes as an axis of symmetry?
If a square has its sides at 45 degree angles to the coordinate axes and one vertex of the square is at (-1,1), then the side length of the square is the 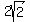 . There are four squares with side length . There are four squares with side length 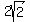 , sides at 45 degree angles to the coordinate axes, and one vertex at the given point (-1,1). How many of them have at least one of the coordinate axes as an axis of symmetry? , sides at 45 degree angles to the coordinate axes, and one vertex at the given point (-1,1). How many of them have at least one of the coordinate axes as an axis of symmetry?
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 5
This diagram shows all the possible squares.

The five possbile squares are
Square PABC (blue)
Square PCDE (blue)
Square PEFG (blue)
Square PHCJ (red)
Square PJEK (red)
The blue squares are all have side lengths of 2 units. The red squares have side lengths of sqrt(2) units.
Note how P is 1 unit above the x axis. Reflecting it over the x axis leads to point C. We can see that segment PC is 2 units long. So that explains why square PABC is 2 by 2, and only one such square is possible where P(-1,1) is in the upper right corner and the sides are vertical. Similar logic applies to the other 2 blue squares.
For the red squares, note how the axis of symmetry lies along the diagonals. If you reflect point E over the y axis, you arrive at point E. Points P and E are sufficient to form square PJEK, where P and E are opposite vertices. So only one red square is possible in this configuration. The other red square PHCJ is a similar story.
|
|
|
| |