|
Question 1163487: How long is the shadow cast on the ground (represented by the xy-plane) by a pole that is eight meters tall, given that the sun’s rays are parallel to the vector [5, 3, −2]?
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How long is the shadow cast on the ground (represented by the xy-plane) by a pole that is eight meters tall,
given that the sun’s rays are parallel to the vector [5, 3, −2]?
~~~~~~~~~~~~~
First, the projection of the given 3D-vector to the (x,y)-plane is the vector V = [5,3].
It defines the direction to the sun in this plane, and its length is | V | =  = = 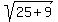 = =  .
Next, if the angle of sun rays with the Earth surface (which we interpret as the plane (x,y)) is .
Next, if the angle of sun rays with the Earth surface (which we interpret as the plane (x,y)) is  , then , then
 = = 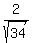 .
From the other side, if L is the shadow length, then .
From the other side, if L is the shadow length, then
 = = 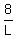 ,
which implies for the shadow length
L = ,
which implies for the shadow length
L = 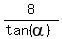 = = 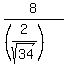 = = 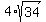 = 23.32 meters (rounded). ANSWER = 23.32 meters (rounded). ANSWER
Solved.
|
|
|
| |