Question 1161458: A triangle has vertices A(3,4), B(-2,0), and C(5,0). Find the midpoint of each side, and label these midpoints D, E, and F.
Verify that the area of triangle ABC is four times the area of triangle DEF
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A triangle has vertices  ( ( , , ), ),  ( ( , , ), and ), and  ( ( , , ). ).
Find the midpoint of each side, and label these midpoints  , , , and , and  . .
the midpoint of  ( ( , , ) and ) and ( ( , , ) is ) is  ( (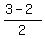 , ,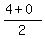 )-> )-> ( ( , , ) )
the midpoint of  ( ( , , ) and ) and  ( ( , , ) is ) is  ( ( , , ) )
the midpoint of  ( ( , , ) and ) and  ( ( , , ) is ) is  ( ( , , ) )

that the area of triangle  is: is:

 = distance between = distance between  and and  which is which is  units units
 = shortest distance between x-axis and = shortest distance between x-axis and 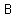 which is which is  units units


 square units square units
the area of triangle 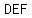 is: is:
base is  -> ->




Verify that the area of triangle  is four times the area of triangle is four times the area of triangle 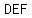 : :

 -> verified -> verified
|
|
|