|
Question 1154317: Find the area of the polygons whose vertices are:
a. (-4, 2), (3, -4), (6, 2), (1, 4)
b. (-3, 4), (1, 5), (4, 2), (3, -3), (-2, -4)
Found 3 solutions by Edwin McCravy, MathTherapy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Since the polygon is convex (has no "sunk-in" places), we make this
determinant of coordinates of vertices, repeating the first one at
the bottom. [It doesn't matter which vertex we start with].
Since the polygon is convex (has no "sunk-in" places), we make this
determinant of coordinates of vertices, repeating the first one at
the bottom. [It doesn't matter which vertex we start with].
 We multiply and add all the "northwest to southeast"-diagonals:
(-4)(-4)+(3)(2)+(6)(4)+(1)(2) = 16+6+24+2=48
We multiply and add all the "northeast to southwest"-diagonals:
(2)(3)+(-4)(6)+(2)(1)+(4)(-4) = 6-24+2-16=-32
Subtract: 48-(-32) = 48+32 = 80
Do the other one the same way. Graph it to make sure it is
a convex polygon. [If the polygon is concave, we would break it
into convex polygons]. If the area comes out negative, just take
the absolute value, making it positive.
Edwin
We multiply and add all the "northwest to southeast"-diagonals:
(-4)(-4)+(3)(2)+(6)(4)+(1)(2) = 16+6+24+2=48
We multiply and add all the "northeast to southwest"-diagonals:
(2)(3)+(-4)(6)+(2)(1)+(4)(-4) = 6-24+2-16=-32
Subtract: 48-(-32) = 48+32 = 80
Do the other one the same way. Graph it to make sure it is
a convex polygon. [If the polygon is concave, we would break it
into convex polygons]. If the area comes out negative, just take
the absolute value, making it positive.
Edwin
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the area of the polygons whose vertices are:
a. (-4, 2), (3, -4), (6, 2), (1, 4)
b. (-3, 4), (1, 5), (4, 2), (3, -3), (-2, -4)
Area of the polygon =  the POSITIVE difference of the SUM of the POSITIVE and NEGATIVE DIAGONAL-PRODUCTS. the POSITIVE difference of the SUM of the POSITIVE and NEGATIVE DIAGONAL-PRODUCTS.
First of all, you have to make sure that the points have been aligned in a CLOCKWISE or COUNTERCLOCKWISE position.
Sum of POSITIVE DIAGONAL-PRODUCTS: - 32
Sum of NEGATIVE DIAGONAL-PRODUCTS: 48

Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Since you have two different answers from two tutors, I came to bring my THIRD solution
(it is a joke, of course : I came to check them).
I consider part (a) only.
In this quadrilateral, we have horizontal diagonal from (-4,2) to (6,2).
It divides the quadrilateral in two triangles.
Their base has the length 10 = 6 - (-4) units.
The upper triangle has the altitude (the height) of 2 = 4 - 2 units.
So, its area is 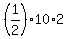 = 10 square units.
The lower triangle has the altitude 6 = 2 - (-4) units.
So, its area is = 10 square units.
The lower triangle has the altitude 6 = 2 - (-4) units.
So, its area is 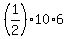 = 30 square units.
Hence, the entire area of the quadrilateral is 10 + 30 = 40 units.
It is the ANSWER to question (a). = 30 square units.
Hence, the entire area of the quadrilateral is 10 + 30 = 40 units.
It is the ANSWER to question (a).
--------------
May I give a fair advise to you ?
In the future, NEVER place more than one problem/question to your post.
It ALWAYS works AGAINST your interests.
|
|
|
| |