SOLUTION: ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=8cm and DF =25cm. Find the length, in cm, of the altitude AG. Diagram: https://

Algebra ->  Length-and-distance -> SOLUTION: ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=8cm and DF =25cm. Find the length, in cm, of the altitude AG. Diagram: https://      Log On


   

Question 1149195: ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=8cm and DF =25cm. Find the length, in cm, of the altitude AG.
Diagram: https://imgur.com/a/l7HBfZY
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.

Connect the points A and D by segment AD and consider triangles ABD and ADC.


Let "a" be the length of the side (of any of the three congruent sides) of the equilateral triangle ABC.



Then the area of the triangle ABD is 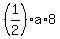 %281%2F2%29%2Aa%2A8,

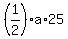and  the area of the triangle ADC is  %281%2F2%29%2Aa%2A25.



The area of the whole triangle ABC is the sum of areas of triangles ABD and ADC


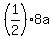    %281%2F2%29%2A8a + %281%2F2%29%2A25a = %281%2F2%29%2Aa%2Aabs%28AG%29.


Cancel the factors  1%2F2  and  "a"  in all three terms, and you will get


    | AG | = 8 + 25 = 33 cm.      ANSWER

Solved.

-----------------

CONCLUSION  and  the  fact  to  MEMORIZE. 

    In any equilateral triangle, the sum of lengths of two perpendiculars from the point in one side 
    to two other sides is equal to the altitude length of the triangle.