|
Question 1133068: Wow I think this is the hardest grade 9 math question!!
In a 6 by 6 grid, how many pathways can be drawn from S to F, (always moving to the right or down) that cross the main diagonal at least once? (You can use the Catalan sequence to answer this question...) The diagram illustrates one pathway that crosses the main diagonal twice.
Link to diagram : http://i63.tinypic.com/2s65wdg.jpg
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Determine the total number of paths from S to F, then subtract the number of paths from S to F that do NOT cross the main diagonal.
(1) To get from S to F moving only right ("R") or down ("D"), you need to have the moves
RRRRRRDDDDDD
in some order. The number of different ways of arranging those letters, and therefore the total number of paths from S to F, is
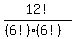 = 12C6 = 924. = 12C6 = 924.
The paths that do NOT cross the main diagonal are of two types: those that always stay below or on the main diagonal, and those that always stay above or on the main diagonal.
There is a symmetry between those two sets of paths; the numbers of paths are the same for both types. So count the number of paths of one of the types; the total number of paths that do not cross the main diagonal is double that number.
To count the number of paths that always stay on or below the main diagonal, draw a picture of the grid (or at least that part of the grid) and label each intersection on the grid with the number of ways to get there:
+---X
| |
1---1---X
| | |
1---2---2---X
| | | |
1---3---5---5---X
| | | | |
1---4---9--14--14---X
| | | | | |
1---5--14--28--42--42---X
| | | | | | |
1---6--20--48--90--132-132
-------------------------------------------------------
Here is a quick description of how those numbers are obtained, in case you don't see it.... Look at the row of numbers 1 - 3 - 5 - 5.
(1) The 1 can only be reached by moving down; there is only 1 way to get the the intersection above, so there is only 1 way to get here.
(2) The 3 can be reached by moving either right or down. There is 1 way to get to the intersection to the left, and there are 2 ways to get to the intersection above; so there are 3 ways to get here.
(3) The first 5 can also be reached by moving either right or down. There are 3 ways to get the the intersection to the left, and there are 2 ways to get to the intersection above; so there are 5 ways to get here.
(4)The second 5 is on the main diagonal, so you can't get here by moving down; you can only get here by moving right. There are 5 ways to get to the intersection to the left, so there are 5 ways to get here.
----------------------------------------------------
We now know that there are 132 paths from S to F that stay on or below the main diagonal; by symmetry there are 132 paths from S to F that stay on or above the main diagonal.
So we have a total of 924 paths from S to F with no restrictions; 132+132=264 of them stay either on or below the main diagonal, or on or above the main diagonal.
So we have our answer:
The number of paths from S to F that cross the main diagonal at least once is 924-264 = 660.
|
|
|
| |