|
Question 1121425: The vertices of a triangle are A(2,4), B(-4,-6), C(6,0), write down the coordinates of P, the midpoint of BC. Find also the coordinates of the points which divide AP internally and externally in the ratio 2:1
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
if  ( ( , ,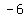 ) and ) and  ( ( , , ), the coordinates of ), the coordinates of  , the midpoint of , the midpoint of 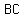 will be will be
 ( (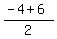 , ,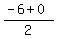 ) )
 ( ( , , ) )
since
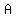 ( ( , , ) )
 ( ( , , ) )
the coordinates of the points which divide 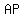 internally and externally in the ratio internally and externally in the ratio 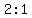 are: are:
use a formula:
if  ( (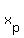 , ,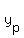 ) divides line segment from ) divides line segment from 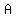 to to  in the ratio in the ratio   , then we have: , then we have:


if  , then we have: , then we have:


substitute given values:










and, your point is  ( ( , ,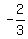 ) )
if divides segment  : :








your point is  ( ( , , ) )
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I personally find the midpoint formulas, and the corresponding formulas for dividing a line segment into a ratio a:b, unpleasant to use, and easy to misuse. While the formulas are valid, it is not easy to understand how they give you the answers.
For me, it is much easier to solve problems like this less formally.
And much more satisfying, because it is easy to see how the results are obtained.
For example, to find the coordinates of p, the midpoint of BC, find how far it is in the x and y directions from B to C, and go half that far.
B to C in the x direction is from -4 to +6, a change of 10; so go halfway: -4+5 = 1. And B to C in the y direction is from -6 to 0, a change of 6; so go halfway: -6+3 = -3.
The coordinates of P are (1,-3).
Now for the points that divide AP internally and externally in the ratio 2:1.
A to P in the x direction is a change of -1; in the y direction is a change of -7.
If Q is the point that divides AP in the ratio 2:1 internally, then AQ = 2*QP. That means Q is 2/3 of the way from A to P. So the x coordinate of Q is 2/3 of the way from 2 to 1: 2 + (2/3)(-1) = 2-2/3 = 4/3. And the y coordinate is 2/3 of the way from 4 to -3: 4 + (2/3)(-7) = 4 - 14/3 = -2/3.
So the coordinates of Q are (4/3,-2/3).
And if R is the point that divides AP in the ratio 2:1 externally, then AR = 2*AP. Since the changes in x and y from A to P are -1 and -7, the changes from A to R meed to be twice that -- -2 and -14.
So the coordinates of R are x = 2+(-2) = 0 and y = 4+(-14) = -10.
|
|
|
| |