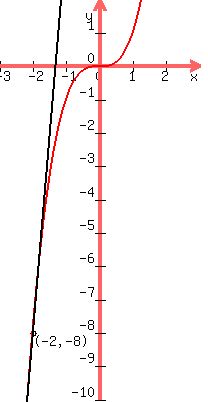
How you go about this problem depends on whether you are in
algebra or calculus. I'll do it both ways. It's much, much
easier by calculus but it can be done by algebra only. Just
for fun, I'll do it both ways, the hard way using algebra
only, and the easy way with calculus. First the hard algebra
way:
1. By algebra only (the hard way).
Let the tangent line have equation y = mx + b
A tangent line must touch the graph at only one point,
so the system of equations:
must have a double solution at x = -2, that is,
it must have multiplicity 2.
Equating the values of y
Substituting x=-2
Substitute for b in
Since the graph goes through the point
where x=-2. the polynomial must be divisible by
x+2.
-2 | 1 0 -m -2m+8
| -2 +4 2m-8
1 -2 -m+4 0
So the polynomial equation factors as
That has a solution of x=-2. But since it must
have a double solution at x=-2, x+2 must also be
a factor of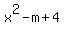 
-2 | 1 -2 -m+4
| -2 8
1 -4 -m+12
The remainder must equal to 0, so
-m+12 = 0
-m = -12
m = 12
So the slope of the tangent line at x=-2 is 12.
------------------
With calculus, it's a cinch!
Substitute x=-2
That's the desired slope.
Edwin
