|
Question 1098180: What is the length of the edge of a cube if after a slice 1cm thick is cut from one side, the volume remaining 294 cubic cm?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE CARPENTER (OR THE CONFIDENT FIFTH-GRADER) SOLUTION:
I know how to calculate the volume of any shoe-box-shaped item.
You just multiply width, length and height.
For a cube, width length and height are all the same edge length.
If the cube edge length was 10 cm,
the initial cube volume would be
(10 cm) X (10 cm) X (10 cm) = 1000 cubic cm.
The volume of the slice cut off would be
(10 cm) X (10 cm) X (1 cm) = 100 cubic cm.
So, the final volume would be 900 cubic cm.
That is more than the 249 cm in the question.
I also know that the larger the original cube,
the larger the final volume,
and the larger the final volume required,
the larger the original cube needed.
What I know tells mne that the original cube edge must be less than 10 cm long.
It also tells me that there is only one answer.
If I calculate using increasing whole number lengths,
the calculated volumes will keep increasing,
so I will get to the answer and 249 cubic cm at some point,
or the answer was not a whole number length, and I will go past the answer.
I can calculate what the volume would be for a few edge lengths to see if I get 249 cubic cm as the answer.
If that happens, I will have the answer.
If not,
I will get less than 249 cubic cm for some whole number edge length,
but more than 249 cubic cm for the next whole number edge length,
and I will know that the answer is somewhere in between.
It is only common sense that the final volume is
more than the volume of a cube with edges 1 cm smaller.
I can easily calculate that a cube with edge length 5 cm has a volume of 125 cubic cm,
so the original cube's edge must be larger than 5 cm.

THE HIGH-SCHOOLER SOLUTION:
If
 = length of the edge of the cube, in cm, = length of the edge of the cube, in cm,
 = volume of the cube in cubic cm, and = volume of the cube in cubic cm, and
 = volume of a slice 1cm thick is cut from one side of the cube. = volume of a slice 1cm thick is cut from one side of the cube.
So,  is the volume remaining, in cubic cm. is the volume remaining, in cubic cm.
All you have to do is solve  <--> <-->  for for  . .
Solving:


It so happens that
 , so , so  is a solution. is a solution.
Is that the only solution?
The way the problwm is worded,
you would think that there is only one solution,
so answering  , ,
and going to the next problem would be a good strategy.
With time and willingless to spare, you could dig deeper
using whatever tools you have.
Using a graphing calculator, you could graph  as as
 and find that and find that  is the only solution. is the only solution.
Using calculus:
 could have 1 or 3 real zeros. could have 1 or 3 real zeros.
 has zeros at has zeros at  and and  , ,
representing respectively a local maximum and a local minimum for  . .
 is the value of is the value of  at its local maximum, at its local maximum,
so  to local maximum to local maximum  , ,
decreases at 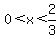 to a local minimum at to a local minimum at  , ,
and then increases for 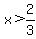 . .
So, there can be only one real zero for  , ,
it happens for some 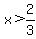 , ,
and as we already found that  is a zero, we know know that is a zero, we know know that  is the only real zero for is the only real zero for  . .
|
|
|
| |