.
The square of the distance from (x,4) to (5,-2) is
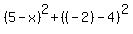 =
= 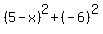 =
= 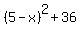 .
The square of the distance from (x,4) to (3,4) is
.
The square of the distance from (x,4) to (3,4) is
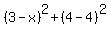 =
= 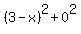 =
= 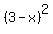 .
So, you need to solve this equation
.
So, you need to solve this equation
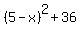 =
= 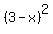 , or
, or
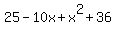 =
=  , or
61 - 10x = 9 - 6x, or
61 - 9 = 10x - 6x,
4x = 52 ====> x =
, or
61 - 10x = 9 - 6x, or
61 - 9 = 10x - 6x,
4x = 52 ====> x = 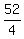 = 13.
= 13.
Answer. x= 13.
Solved.