|
Question 1067878: Find the equation of a circle that has radius length {sqrt(30)} and is tangent to the line 3x+y-5=0 at the point (-1,8).
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There will be two solutions because the circle could be on either
side of the line.
The equation of a circle is:
(x-h)² + (y-k)² = r² with center (h,k) and radius r.
The radius is the distance from (h,k) to (-1,8).
We use the distance formula:
  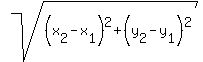
  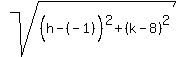
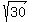  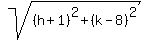 Square both sides:
Square both sides:
  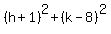 The radius
The radius 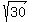 is also the perpendicular distance from
(h,k) to the line 3x+y-5=0
We use the formula:
The perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is d = is also the perpendicular distance from
(h,k) to the line 3x+y-5=0
We use the formula:
The perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is d = 
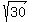 = = 
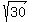 = = 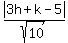
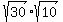 = = 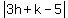
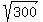 = = 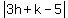
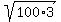 = = 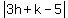
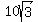 = = 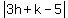
 = = 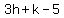
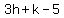  
   Substitute in
Substitute in
  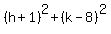
   There is a lot of work here! I'm not going to type the
steps. But you square those out and use the quadratic
formula.
Use the + and solve for h and get
There is a lot of work here! I'm not going to type the
steps. But you square those out and use the quadratic
formula.
Use the + and solve for h and get  then
then
 Then substitute that in:
Then substitute that in:
  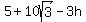
  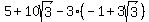
  
  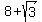 So the center of one circle is
(h,k) =
So the center of one circle is
(h,k) = 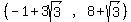
 To find the equation we substitute for h,k, and r in
To find the equation we substitute for h,k, and r in


 Using the - sign, and doing the same thing:
(h,k) =
Using the - sign, and doing the same thing:
(h,k) = 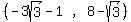
 You can get the equation of that circle the same way.
You can get the equation of that circle the same way.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the equation of a circle that has radius length {sqrt(30)} and is tangent to the line 3x+y-5=0 at the point (-1,8).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I think that more short (and more straightforward) solution is possible.
The idea is to draw (to write the equation of) the straight line perpendicular to the given line through the given point (-1,8),
and then to take its intersection with the circle of the radius 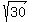 centered at the given point (-1,8). centered at the given point (-1,8).
 Plot y = 5-3x (the given line, red), y =
Plot y = 5-3x (the given line, red), y = 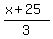 (the perpendicular at (-1,8), green)
and the circle centers (intersection points of the green straight line with the arcs, blue and purple arcs)
1. The straight line perpendicular to the given line 3x+y-5=0 at the point (-1,8) is
-(x-(-1)) + 3(y-8) = 0, or (which is the same) -x - 1 + 3y - 24 = 0 or (which is equivalent) x = 3y-25.
2. The circle of the radius (the perpendicular at (-1,8), green)
and the circle centers (intersection points of the green straight line with the arcs, blue and purple arcs)
1. The straight line perpendicular to the given line 3x+y-5=0 at the point (-1,8) is
-(x-(-1)) + 3(y-8) = 0, or (which is the same) -x - 1 + 3y - 24 = 0 or (which is equivalent) x = 3y-25.
2. The circle of the radius 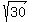 centered at (-1,8) is centered at (-1,8) is
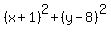 = =  .
3. The centers of two circles we are searching for, are the intersection points, i.e. the solutions of the system
x = 3y-25, (1) .
3. The centers of two circles we are searching for, are the intersection points, i.e. the solutions of the system
x = 3y-25, (1)
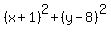 = =  . (2)
To solve the system, substitute (1) into (2), replacing x. You will get . (2)
To solve the system, substitute (1) into (2), replacing x. You will get
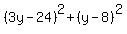 = 30,
9y^2 - 144y + 576 + y^2 - 16y + 64 = 30,
10y^2 - 160y + 610 = 0, = 30,
9y^2 - 144y + 576 + y^2 - 16y + 64 = 30,
10y^2 - 160y + 610 = 0,
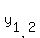 = = 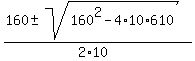 = = 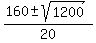 = = 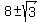 .
Thus the centers are
a) .
Thus the centers are
a)  = = 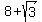 , ,  = 3y-25 = = 3y-25 = 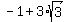 , and
b) , and
b)  = = 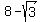 , ,  = 3y-25 = = 3y-25 = 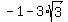 . .
Having the centers and the radius r = 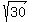 , everybody can write the standard equations for the two circles. , everybody can write the standard equations for the two circles.
|
|
|
| |