|
Question 1058420: A one compartment vertical file is to be constructed by bending the long side of an 8 in by 12 in. sheet of plastic along two lines to form a U shape. How tall should the file be to maximize the volume that it can hold?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The cross section would be a squared up U, with vertical sides  inches tall, inches tall,
and a middle horizontal section 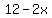 inches wide. inches wide.
We really want to maximize the cross section area of the  by by 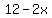 rectangle, rectangle,
because the 8 inch depth of the file is determined by the width of the 8 in by 12 in sheet of plastic.
The area of that cross section is
 or or 
That is a polynomial of degree 2, or in other words a quadratic function.
We know that those are symmetrical functions with a minimum or maximum at their axis of symmetry (at the vertex of the parabola).
That maximum has to be exactly halfway between the zeros of the function,
which we knew would be at  and (((x=6}}} before writing anything, and (((x=6}}} before writing anything,
because those values correspond to no vertical sides, and no horizontal bottom respectively.
So, the file should be  inches tall. inches tall.
What did your teacher expect?
Maybe calculating volume as



and after that,
either calculating the derivative to find the  value for the maximum, value for the maximum,
or using the "formula" 
to find the axis of symmetry of a quadratic function
 . .
|
|
|
| |