Question 1045419: find the area of a triangle with the vertices ( 7.-9), (-1,6),(-1,-9)
Found 3 solutions by josgarithmetic, advanced_Learner, MathTherapy:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use the length from (7,-9) to (-1,-9) as a base of the triangle.
Use the length from (-1,6) to (-1,-9) as the height of the triangle.
If b is BASE and h is HEIGHT, then formula for area of a triangle is  . .
Answer by advanced_Learner(501)   (Show Source): (Show Source):
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
find the area of a triangle with the vertices ( 7.-9), (-1,6),(-1,-9)
Let points (7, - 9), (- 1, 6), and (- 1, - 9) be A, B, and C, respectively
We then have: A(7, - 9), B(- 1, 6), C(- 1, - 9)
Line AC is parallel to the x-axis, and so, its length is: 7 - - 1, or 7 + 1, or 8 units
Line BC is parallel to the y-axis, and so, its length is: 6 - - 9, or 6 + 9, or 15 units
We now see that the polygon is a right-triangle, and that AC and BC are its legs.
Therefore, area = 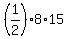 , or , or 
|
|
|