|
Question 1040749: Hello amazing tutors, can you help me solve this pleasee, thank youuu
(i)Sketch the graph of the curve y = 3 sin x, for −π ≤ x ≤ π
The straight line y = kx, where k is a constant, passes through the maximum point of this curve for −π ≤ x ≤ π .
(ii) Find the value of k in terms of π
(iii) State the coordinates of the other point, apart from the origin, where the line and the curve
intersect
Found 2 solutions by robertb, josmiceli:
Answer by robertb(5830)   (Show Source): (Show Source):
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The basic facts you need to know about
the sine curve is:
(1) 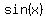 repeats itself every repeats itself every 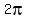
radians
(2) the maximum value of 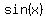 is is 
and this maximum occurs every 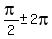
radians
-----------------------------------------
(i), (ii), and (iii)
You are given the interval −π ≤ x ≤ π
so, the only place where there is a maximum in this
interval is: 
------------------------
Your sine function is 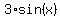 , the the maximum is , the the maximum is
 . Now you know the maximum point is at . Now you know the maximum point is at
( pi/2, 3 )
------------------
The straight line  must also pass through that must also pass through that
point and also (0,0) since  gives you (0,0) gives you (0,0)
-------------------
The slope, 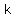 , is , is  , so the equation is: , so the equation is:

-------------------
Here are plots of
 and and

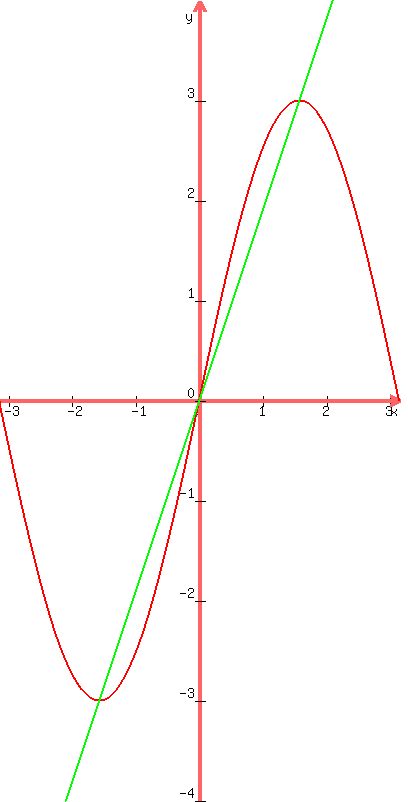
|
|
|
| |