SOLUTION: If a straight line passes through the point (2,4), find the locus of the middle point of the segment of the line intercepted between the axes

Algebra ->  Length-and-distance -> SOLUTION: If a straight line passes through the point (2,4), find the locus of the middle point of the segment of the line intercepted between the axes      Log On


   

Question 1019640: If a straight line passes through the point (2,4), find the locus of the middle point of the segment of the line intercepted between the axes
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
We use the following form of the straight line: x%2Fa+%2B+y%2Fb+=+1, where a is the value of the x-intercept and b is the value of the y-intercept.
The equation of the straight line passing through the point (2,4) is given by 2%2Fa+%2B+4%2Fb+=+1 as per the previous statement.
Solving for b in terms of a,
4%2Fb+=+1-2%2Fa,
==> 4%2Fb+=+%28a-2%29%2Fa
==> b%2F4+=+a%2F%28a-2%29
==> b+=+%284a%29%2F%28a-2%29. (Equation A)
This gives the relationship between the x- and y-intercepts of the line.
Now the midpoint of the x-intercept (a,0) and the y-intercept (0,b) is the point (a/2, b/2).
Substituting Equation A into the y-coordinate of the point (a/2, b/2), we get
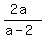(a%2F2, %282a%29%2F%28a-2%29)
Now let x = a/2 and y = 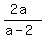%282a%29%2F%28a-2%29
==> a = 2x
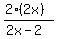
==> y = %282%282x%29%29%2F%282x-2%29
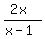
==> y = %282x%29%2F%28x-1%29
This is the equation of the locus satisfying the given conditions.
This is a hyperbola with horizontal asymptote of y = 2, and vertical asymptote of x = 1.