|
Question 1010001: Find the coordinates of the point that is equidistant from (-2,5), (8,5), and (6,7).
Found 2 solutions by stanbon, KMST:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the coordinates of the point that is equidistant from
(-2,5), (8,5), and (6,7).
-----
From (-2,5)::sqrt[(x+2)^2+(y-5)^2]
From (8,5):: sqrt[(x-8)^2+(y-5)^2]
From (6,7):: sqrt[(x-6)^2+(y-7)^2]
------
Equate rows 1 and 2::
(x+2)^2 = (x-8)^2
x^2 + 4x + 4 = x^2 - 16x + 64
-----
4x + 4 = -16x + 64
20x = 60
x = 3
----
Solve for "y"::
Equate rows 2 and 3
-----
(x-8)^2 + (y-5)^2 = (x-6)^2 + (y-7)^2
----
Since x = 3::
5^2 + y^2 - 10y + 25 = 3^2 + y^2 - 14y + 49
------
4y + 50 = 58
---
4y = 8
y = 2
----
Ans: (3,2)
--------------
Cheers,
Stan H.
--------
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE CONCEPTS NEEDED:
Three points (such as 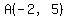 , , 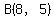 and and 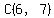 )determine a triangle. )determine a triangle.
 and I bet the circumcenter of a triangle was mentioned in your math class. and I bet the circumcenter of a triangle was mentioned in your math class.
I do not advocate memorizing lists of words for the sake of memorizing,
but the teacher will expect you to remember that word (and many others).
The circumcenter is a point that is equidistant from all three vertices of the triangle.
If you draw a circle centered at that point,
using the distance to a vertex as the radius,
all three vertices are on that circle,
and the rest of the triangle is inside the circle.
The circle goes all around the triangle as tightly as possible,
and that is why its center point is called the circumcenter of the triangle.

All the points equidistant from 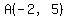 , and , and 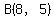 are in the perpendicular bisector of segment are in the perpendicular bisector of segment  . .
The perpendicular bisector of a segment is the perpendicular line that bisect the segment
(meaning that it divides the segment into two pieces of equal length).
It goes through the midpoint of the segment.
All the points equidistant from 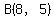 , and , and 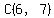 are in the perpendicular bisector of segment are in the perpendicular bisector of segment  . .
So, the point equidistant from 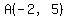 , , 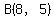 and and 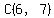
is where those two bisectors intersect.
(The bisector of  also goes through that point, also goes through that point,
but we do not need it to solve the problem.
THE WAY TO "SEE" AND UNDERSTAND THE PROBLEM:
After drawing the triangle, I saw that  was a "horizontal" segment was a "horizontal" segment
(meaning parallel to the x-axis),
so I realized that a line perpendicular to  was going to be a "vertical" line was going to be a "vertical" line
(meaning parallel to the y-axis).
I also saw that the midpoint of  was was 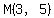 . .
So I could easily draw the perpendicular bisector of segment  : :

I also so that  was one of the diagonals of two squares on the grid, was one of the diagonals of two squares on the grid,
so a line perpendicular to that line was going o be a diagonal of squares slanted in the opposite direction.
It was also easy to see that the mid point of the segment between 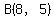 and and 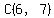
is 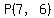 . .
So I drew  and the perpendicular bisector of and the perpendicular bisector of  : :
 and at the intersection of those two perpendicular bisectors I found and at the intersection of those two perpendicular bisectors I found  , ,
the point equidistant from 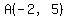 , , 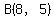 and and 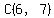 . .
IF YOU HAVE TO SHOW THE FANCY FOOTWORK:
The coordinates of the midpoint of a segment are found by averaging the coordinates of the endpoints of the segment.
In fancy formulas, for points 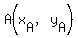 and and 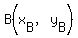 , the midpoint is , the midpoint is 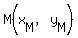 , ,
with  and and  . .
So, for points 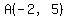 and and 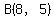 , the coordinates of , the coordinates of  are are
 and and  , ,
and for points 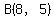 and and 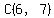 , the coordinates of midpoint , the coordinates of midpoint  are are
 and and  . .
The perpendicular bisector to horizontal segment  , that is part of the line with equation , that is part of the line with equation  , ,
is a vertical line with equation  that goes through that goes through 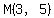 . .
Therefore the equation of the perpendicular bisector to segment  is is  . .
To find the perpendicular bisector to a segment that is neither vertical nor horizontal,
such as  , you have to deal with slopes. , you have to deal with slopes.
The slope of  is calculated as is calculated as
 . .
The slope of a line perpendicular to  is is
 . .
The perpendicular bisector to  is the line with slope is the line with slope 
passing through  , ,
which can be written in slope-point form as
 and substituting we get and substituting we get
 <--> <--> <--> <--> <--> <--> . .
The point we look is at the intersection of both perpendicular bisectors, so it is the solution to
 --> --> . .
|
|
|
| |