|
Question 1004861: Find the point on each median that is two-thirds of the distance from the vertec to the midpoint if the vertices of the triangle are A (4,-4), B (10,4) & C (2,6)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! The midpoints are
(7,0),(6,5),(3,1)

The midpoint of the triangle is 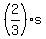 the length of the median. the length of the median.
Find one vertex, and go 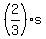 the way to the midpoint of the opposite side. Directions matter. Start at the point, and take the way to the midpoint of the opposite side. Directions matter. Start at the point, and take 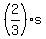 the the  value and value and 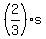 the the  value. value.
The easiest one is 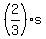 from ( from ( , , ) to ( ) to ( , , ) )
The  -value is -value is 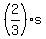 from from  to to  . The distance is . The distance is  , and , and 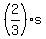 of that is of that is 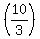 , or , or 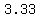 . .
So the  -value is -value is 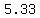 or or 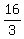 . .
The  -value is -value is 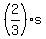 from from  to to  , or , or  . The . The  -value is -value is  . .
The midpoint is (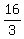 , , ). ).
This will work for the other two points to the opposite side midpoint.
or, you can do it this way:
take two vertices and two midpoints and find the equations of the lines passing through one midpoint and opposite vertices
R(7,0) and C (2,6)
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (7, 0) and (x2, y2) = (2, 6).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(-1.2)x + (8.4)
Your graph:

|
Q(6,5) and A (4,-4)
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (6, 5) and (x2, y2) = (4, -4).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(4.5)x + (-22)
Your graph:

|
so, your equations are:
 and and

-----------------find intersection
since left sides equal, make right sides equal and solve for 






find 





intersection point is at (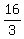 , , ) and that is your midpoint ) and that is your midpoint

|
|
|
| |