|
Tutors Answer Your Questions about Length-and-distance (FREE)
Question 1176989: EVOL is a cyclic quadrilateral, inscribed in a circle with center S. Given that the radius of this circle is 25 in. and angle VEL is 55 degrees, explain your work to find the following measurements.
a)Length of Major Arc VL
b)Angle measure of Minor Arc VL
c)Angle VOL
d)Length of Chord VL
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52747)   (Show Source): (Show Source):
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! You got it! Let's go through the problem again, with a focus on clear explanations.
**Understanding the Setup**
* **EVOL is a cyclic quadrilateral:** This means that all four points (E, V, O, L) lie on the circumference of a circle.
* **Center S:** The point S is the exact center of the circle.
* **Radius = 25 inches:** The distance from the center S to any point on the circle's edge (E, V, O, or L) is 25 inches.
* **Angle VEL = 55 degrees:** This is an inscribed angle, meaning its vertex (E) lies on the circle.
**Solving the Problem**
**a) Length of Major Arc VL**
1. **Find Angle VOL (The Central Angle):**
* A central angle is an angle formed by two radii of a circle, with its vertex at the center.
* The measure of a central angle is twice the measure of an inscribed angle that intercepts the same arc.
* Since angle VEL intercepts arc VL, and angle VOL also intercepts arc VL, we have:
* Angle VOL = 2 * Angle VEL = 2 * 55 degrees = 110 degrees.
* This 110 degrees is the measure of the *minor* arc VL.
* The *major* arc VL is the rest of the circle. So:
* Major arc VL = 360 degrees - 110 degrees = 250 degrees.
2. **Calculate the Circumference:**
* The circumference (the total distance around the circle) is found using the formula:
* Circumference = 2 * π * radius
* Circumference = 2 * π * 25 inches = 50π inches.
3. **Find the Length of the Major Arc:**
* The length of an arc is a fraction of the circle's circumference, determined by the arc's central angle.
* Length of Major Arc VL = (Central Angle of Major Arc / 360 degrees) * Circumference
* Length of Major Arc VL = (250 degrees / 360 degrees) * 50π inches
* Length of Major Arc VL = (25/36) * 50π inches = 1250π/36 inches = 625π/18 inches.
* This is approximately 109.08 inches.
**b) Angle Measure of Minor Arc VL**
* The angle measure of a minor arc is the same as the measure of the central angle that intercepts it.
* Therefore, the angle measure of minor arc VL is 110 degrees.
**c) Angle VOL**
* We already calculated this in part (a).
* Angle VOL = 110 degrees.
**d) Length of Chord VL**
1. **Visualize Triangle VOL:**
* Connect points V and L with a straight line (the chord VL).
* Triangle VOL is formed by the radii SV and SL, and the chord VL.
* Because SV and SL are radii, they are equal in measure, therefore triangle VOL is an isosceles triangle.
2. **Use the Law of Cosines:**
* The Law of Cosines is used to find a side length in a triangle when you know two side lengths and the included angle.
* In triangle VOL:
* VO = 25 inches (radius)
* LO = 25 inches (radius)
* Angle VOL = 110 degrees
* The Law of Cosines formula is: VL² = VO² + LO² - 2 * VO * LO * cos(Angle VOL)
* VL² = 25² + 25² - 2 * 25 * 25 * cos(110 degrees)
* VL² = 625 + 625 - 1250 * (-0.3420) (approximately)
* VL² = 1250 + 427.5 = 1677.5
* VL = √1677.5 ≈ 40.96 inches.
**Summary**
* **a) Length of Major Arc VL:** 625π/18 inches (approximately 109.08 inches)
* **b) Angle Measure of Minor Arc VL:** 110 degrees
* **c) Angle VOL:** 110 degrees
* **d) Length of Chord VL:** Approximately 40.96 inches
Question 1186272: On a wall, 60 1/2 cm wide, Oscar is going to hang three pictures beside each other, each measuring 9 1/3 cm wide. He will leave 3 1/2 cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture, and will centre these nails leaving 4 cm between each pair. How far, in cm, from the end of the wall(on either side) will the first nail be placed?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
On a wall, 60 1/2 cm wide, Oscar is going to hang three pictures beside each other, each measuring 9 1/3 cm wide.
He will leave 3 1/2 cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture,
and will centre these nails leaving 4 cm between each pair. How far, in cm, from the end of the wall(on either side)
will the first nail be placed?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution and the answer in the post by @CPhill are incorrect.
Below is my correct solution.
**1. Calculate the total width of the pictures:**
* Each picture is 9 1/3 cm wide.
* Three pictures have a total width of 9 1/3 cm * 3 = 28 cm
**2. Calculate the total width of the spaces between pictures:**
* There are two spaces between the three pictures.
* Each space is 3 1/2 cm wide.
* The total width of the spaces is 3 1/2 cm * 2 = 7 cm
**3. Calculate the total width of the pictures and spaces:**
* The combined width of the pictures and spaces is 28 cm + 7 cm = 35 cm
**4. Calculate the remaining space on either side of the wall:**
* The wall is 60 1/2 cm wide, which is 60.5 cm.
* The space left on both sides of the wall is 60.5 cm - 35 cm = 25.5 cm
* Since the space is split equally on both sides, each side has 25.5 cm / 2 = 12 3/4 cm
**5. Calculate the distance from the end of the wall to the first nail:**
* The distance to the first nail is the space on either side plus half the width of a picture minus 2 cm
(2 cm is half the space between the nails placement).
* Distance = 12 3/4 cm + (9 1/3 cm / 2) - 2 cm
* Distance = 12 3/4 cm + 4 2/3 cm - 2 cm
* Distance = 15 5/12 cm, or 15.42 cm (rounded decimal)
**Therefore, the first nail will be placed 15 5/12, or 15.42 cm from the end of the wall.**
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**1. Calculate the total width of the pictures:**
* Each picture is 9 1/3 cm wide, which is 9.33 cm in decimal form.
* Three pictures have a total width of 9.33 cm * 3 = 27.99 cm
**2. Calculate the total width of the spaces between pictures:**
* There are two spaces between the three pictures.
* Each space is 3 1/2 cm wide, which is 3.5 cm.
* The total width of the spaces is 3.5 cm * 2 = 7 cm
**3. Calculate the total width of the pictures and spaces:**
* The combined width of the pictures and spaces is 27.99 cm + 7 cm = 34.99 cm
**4. Calculate the remaining space on either side of the wall:**
* The wall is 60 1/2 cm wide, which is 60.5 cm.
* The space left on both sides of the wall is 60.5 cm - 34.99 cm = 25.51 cm
* Since the space is split equally on both sides, each side has 25.51 cm / 2 = 12.755 cm
**5. Calculate the distance from the end of the wall to the first nail:**
* The distance to the first nail is the space on either side plus half the width of a picture plus 4 cm for the nail placement.
* Distance = 12.755 cm + (9.33 cm / 2) + 4 cm
* Distance = 12.755 cm + 4.665 cm + 4 cm
* Distance = 21.42 cm
**Therefore, the first nail will be placed 21.42 cm from the end of the wall.**
Question 1210282: The distance between Miami and Orlando is about 220 miles. A pilot flying from Miami to Orlando starts the flight 10degrees off course to avoid a storm. If the pilot adjusts his course after 100 miles, how much farther is the flight than a direct route?
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The distance between Miami and Orlando is about 220 miles. A pilot flying from Miami to Orlando
starts the flight 10 degrees off course to avoid a storm. If the pilot adjusts his course
after 100 miles, how much farther is the flight than a direct route?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let point M represents Miami, point O represents Orlando, and let point C represents
the point where the pilot adjusts/changes the course.
So, we have triangle MOC on a plane (surely, we consider the Earth surface as flat
in this problem).
In triangle MOC, side MO is 220 miles (the distance from Miami to Orlando);
side MC is 100 miles (given) and the concluded angle OMC is 10 degrees.
Let's apply the cosine law to find the side CO of this triangle. We have then
CO =  = =  = 122.753 miles (rounded).
The problem asks how longer is the sum MC + CO than MO. So, we calculate
MC + CO - MO = 100 + 122.753 - 220 = 2.753 miles.
ANSWER. The flight is 2.753 miles longer than the direct root. = 122.753 miles (rounded).
The problem asks how longer is the sum MC + CO than MO. So, we calculate
MC + CO - MO = 100 + 122.753 - 220 = 2.753 miles.
ANSWER. The flight is 2.753 miles longer than the direct root.
Solved.
Thanks for posting this problem.
I appreciate the accuracy of your post and clear language of your message.
It is a rare case in our days.
Question 1210281: a 50m supporting wire is to be attached to a 75 m antenna. Because of surrounding buildings, sidewalks, and roadways, the wire must be anchored exactly 20 m from the base of the antenna. How high from the top of the antenna is the wire attached?
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a 50m supporting wire is to be attached to a 75 m antenna. Because of surrounding buildings,
sidewalks, and roadways, the wire must be anchored exactly 20 m from the base of the antenna.
How high from the top of the antenna is the wire attached?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let 'x' be the height of attaching the wire, from the ground.
We have a right-angled triangle "the ground - the antenna - the wire".
From this right-angled triangle,
x^2 + 20^2 = 50^2,
x^2 = 50^2 - 20^2 = 2500 - 400 = 2100
x = 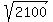 = 45.83 meters (rounded).
So, the distance of attaching from the top of the antenna is
75 - 45.83 = 29.17 meters. ANSWER = 45.83 meters (rounded).
So, the distance of attaching from the top of the antenna is
75 - 45.83 = 29.17 meters. ANSWER
Solved.
Thanks for posting this problem.
I appreciate the accuracy of your post and clear language of your message.
Question 1210201: Let ABCD be a square with side length 1. A laser is located at vertex A, which fires a laser beam at point X on side BC, such that BX = 2/3. The beam reflects off the sides of the square, until it ends up at another vertex; at this point, the beam will stop. Find the length of the total path of the laser beam. The diagram is linked below
https://artofproblemsolving.com/texer/zqcbfanp
Found 5 solutions by mccravyedwin, AnlytcPhil, ikleyn, greenestamps, CPhill:
Answer by mccravyedwin(405)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I think this particular AI system is getting better! That's the way AI works.
AI systems are programmed to learn from their mistakes.
When AI chess programs started out, anybody could beat them who knew the rules of
chess. But now no human chess master is able to beat the most sophisticated
AI chess programs.
Making mistakes and correcting them is essential for learning. If you only learn
the best ways first, you never learn why the other ways are inferior.
Edwin
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I think this particular AI system is getting better! That's the way AI works.
AI systems are programmed to learn from their mistakes.
When AI chess programs started out, anybody could beat them who knew the rules of
chess. But now no human chess master is able to beat the most sophisticated
AI chess programs.
Making mistakes and correcting them is essential for learning. If you only learn
the best ways first, you never learn why the other ways are inferior.
Edwin
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let ABCD be a square with side length 1. A laser is located at vertex A, which fires a laser beam
at point X on side BC, such that BX = 2/3. The beam reflects off the sides of the square,
until it ends up at another vertex; at this point, the beam will stop.
Find the length of the total path of the laser beam. The diagram is linked below
https://artofproblemsolving.com/texer/zqcbfanp
~~~~~~~~~~~~~~~~~~~~~~~~
Couple of notices before to start.
(a) The link is EMPTY and does not show/(does not contain) any picture/diagram.
(b) The solution and all calculations in the post by @CPhill are WRONG.
I came to bring a correct solution.
(1) First beam goes from A to X on BC.
One leg is 1 unit, other leg is 2/3 of the unit.
Hence, AX =  = =  = =  (2) Then the beam reflects at X on BC and goes to point Y on DC.
The angle of incidence at X is equal to the angle of reflection at X.
Hence, right-angled triangles ABX and XCY are similar.
The similarity coefficient is BX/XC =
(2) Then the beam reflects at X on BC and goes to point Y on DC.
The angle of incidence at X is equal to the angle of reflection at X.
Hence, right-angled triangles ABX and XCY are similar.
The similarity coefficient is BX/XC =  = 2.
Hence, XY is half of AX. i.e. = 2.
Hence, XY is half of AX. i.e.  .
(3) Next, the beam reflects at Y on DC and goes to point Z on AD.
Again, the angle of incidence at Y is equal to the angle of reflection at Y.
Hence, right-angled triangles XCY and YDZ are similar.
The similarity coefficient is CY/YD = .
(3) Next, the beam reflects at Y on DC and goes to point Z on AD.
Again, the angle of incidence at Y is equal to the angle of reflection at Y.
Hence, right-angled triangles XCY and YDZ are similar.
The similarity coefficient is CY/YD =  = 1.
So, the triangles XCY and YDZ are not only similar - - - they are CONGRUENT.
It implies that DZ = 1/3 and ZY = XY = = 1.
So, the triangles XCY and YDZ are not only similar - - - they are CONGRUENT.
It implies that DZ = 1/3 and ZY = XY =  .
(4) Now point Z is symmetric to point X.
It means that after next reflection at Z, the beam will go directly to vertex B.
and the journey will be complete.
The last beam's interval YB is the same long as AZ, i.e. .
(4) Now point Z is symmetric to point X.
It means that after next reflection at Z, the beam will go directly to vertex B.
and the journey will be complete.
The last beam's interval YB is the same long as AZ, i.e.  .
(5) The last step is to find the total length of the journey
AX + XY + YZ + ZB = .
(5) The last step is to find the total length of the journey
AX + XY + YZ + ZB =  + +  + +  + +  = =  , or about 3.60555.
It is the ANSWER to the problem's question. , or about 3.60555.
It is the ANSWER to the problem's question.
Solved.
The work and the calculations in the post by @CPhill
amaze me with their low level.
His work/technique is at the level of a student,
whose scores are between 2 and 3 in the five-score scale.
Closer to 2 than to 3.
The true AI level should be 6 + + +.
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Your link does not show a diagram....
The AI solution from the other tutor is wrong. That solution says the ray hits vertex D after the single reflection off side BC. That will not happen if the length of BC is 2/3. (Note that, by symmetry, the ray would hit vertex D after the single reflection off side BC if the length of BX were 1/2 instead of 2/3.)
Let Y be the point on CD where the ray hits after reflecting off side BC.
Since the angle of reflection is the same as the angle of incidence, triangles ABX and YCX are similar. Since BX is 2/3 and CX is 1/3, the ratio of similarity between the two triangles is 2:1.
But then, by that ratio of similarity, CY is half the length of AB, which is a side of the square. So Y is the midpoint of CD.
From there, we can see by symmetry that the ray will reflect off side CD and continue to vertex B.
Here is a diagram, with the path of the ray in red, starting from vertex A and ending at vertex B.

From the Pythagorean Theorem with AB=1 and BX=2/3, the length of AX is  . .
Because of the similarity of triangles ABX and YCX, the length of XY is  . .
That makes the length of the path of the ray from A to X to Y  . .
And then by symmetry the path from Y to side AD and then on to vertex B is again  . .
So the total length of the path from vertex A to vertex B, reflecting off sides BC, CD, and DA, is  . .
ANSWER: 
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the square \( ABCD \) be oriented in the coordinate plane with points defined as follows:
- \( A = (0, 1) \)
- \( B = (0, 0) \)
- \( C = (1, 0) \)
- \( D = (1, 1) \)
The laser beam is fired from point \( A \) at an angle towards point \( X \), where \( X \) is the point on side \( BC \) such that \( BX = \frac{2}{3} \). The coordinates of point \( X \) are given by:
\[
X = (0, \frac{2}{3})
\]
To find the direction of the laser beam from \( A \) to \( X \), we calculate the vector from \( A \) to \( X \):
\[
\overrightarrow{AX} = X - A = (0, \frac{2}{3}) - (0, 1) = (0, -\frac{1}{3})
\]
The slope of this line is
\[
\text{slope} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\frac{2}{3} - 1}{0 - 0} \quad \text{(vertical line)}.
\]
For the moment, let us compute the direct distance from \( A \) to \( X \):
\[
d_{AX} = \sqrt{(0 - 0)^2 + \left(\frac{2}{3} - 1\right)^2} = \sqrt{0 + \left(-\frac{1}{3}\right)^2} = \frac{1}{3}.
\]
The laser beam will reflect off of side \( BC \) and into side \( CD \). The point X is at a vertical location of \( \frac{2}{3} \) from the bottom of the square.
Now let's consider what happens when it reflects off side \( BC \). The line from \( A \) to \( X \) intersects \( BC \) at \( X \), and then heads towards side \( CD \).
The angle of incidence equals the angle of reflection. After reflecting off side \( BC \), the beam will change its direction but maintain its angle of slope towards the other vertical wall, \( CD \).
The horizontal direction can be preserved by extending or 'unfolding' the square. The strategy involves reflecting the square:
1. From \( A \) to \( X \), the laser hits \( BC \).
2. It then reflects and heads towards \( D \), calculating where it hits before potentially hitting at \( D \).
With this reflection, the new direction of travel can be calculated using the symmetry of the reflections:
- Upon reflecting, after reaching \( BC \) it would travel back upwards towards \( CD \) (at point \( D \)), moving rightward.
The distance until it would again meet the line \( AD \):
1. From \( X \) to \( D \) directly makes up the next segment. The coordinates for \( D \) are \( (1, 1) \) when revisiting from \( (0, \frac{2}{3}) \):
This results in:
\[
d_{XD} = \sqrt{(1 - 0)^2 + (1 - \frac{2}{3})^2} = \sqrt{1^2 + \left(\frac{1}{3}\right)^2} = \sqrt{1 + \frac{1}{9}} = \sqrt{\frac{10}{9}} = \frac{\sqrt{10}}{3}.
\]
Total distance:
\[
d_{AX} + d_{XD} = \frac{1}{3} + \frac{\sqrt{10}}{3} = \frac{1 + \sqrt{10}}{3}.
\]
Thus, the total path of the laser beam from A to D via reflections is
1 + \sqrt{10}.
Question 1166192: Charlie has a collection of books that he wishes to display in a narrow
bookcase with shelves of width 56 cm. The thickest books are no more
than 16 cm wide and, when placed side by side, the entire collection takes
up 2.4m. Find, with justification, the minimum number of shelves required
to guarantee that all of the books can be displayed in the bookcase.
I'm confused with how to justify this. Can someone please help me? Thanks!
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Charlie has a collection of books that he wishes to display in a narrow bookcase with shelves of width 56 cm.
The thickest books are no more than 16 cm wide and, when placed side by side, the entire collection takes up 2.4m.
Find, with justification, the minimum number of shelves required to guarantee
that all of the books can be displayed in the bookcase.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve the problem in two steps.
First, I will show that for some special case under the condition, 5 shelves are not enough.
Then I will prove that 6 shelves are enough for any case under the condition.
Let all the books are 15 cm wide.
Then the total number of books is  = 16,
and we can place ONLY 3 such books at each shelf.
So, having 5 shelves, we can place only 3*5 = 15 such books, and we need then
the 6-th shelf for the 16-th book. = 16,
and we can place ONLY 3 such books at each shelf.
So, having 5 shelves, we can place only 3*5 = 15 such books, and we need then
the 6-th shelf for the 16-th book.
Now, after completing this case, I can solve the problem in full.
My statement is that 6 shelves is always enough.
1) In the 1-st shelf, I can fill at least 40 cm of 56 cm.
Indeed, if less than 40 cm is filled, then I can add any book (since it is no
thicker than 16 cm).
2) In the 2-nd shelf, I can fill at least 40 cm of 56 cm.
Indeed, if less than 40 cm is filled, then I can add any book (since it is no
thicker than 16 cm).
3) In the 3-rd shelf, I can fill at least 40 cm of 56 cm.
Indeed, if less than 40 cm is filled, then I can add any book (since it is no
thicker than 16 cm).
4) In the 4-th shelf, I can fill at least 40 cm of 56 cm.
Indeed, if less than 40 cm is filled, then I can add any book (since it is no
thicker than 16 cm).
5) In the 5-th shelf, I can fill at least 40 cm of 56 cm.
Indeed, if less than 40 cm is filled, then I can add any book (since it is no
thicker than 16 cm).
6) In the 6-th shelf I can fill at least 40 cm of 56 cm.
Indeed, if less than 40 cm is filled, then I can add any book (since it is no
thicker than 16 cm).
So, I can fill at least 40 cm of 56 cm in each of 6 shelves.
Taken together, 6 times 40 cm comprise 2 m 40 cm,
which means that ALL the books will be placed in 6 shelves.
***********************************
THE PROOF IS COMPLETED.
***********************************
It is a TRUE Math Olympiad level Math problem (!)
Question 1171645: 1)Find DE 2x-6 ,x-1 , 14
2)Find x if m
3)m
4)m
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1173735: Airport B is 320 miles from airport A on a bearing of S40°E. A pilot wishes to fly from A to B, but to avoid a storm must first fly due East at a speed of 210 mph for an hour, and then from this point (call it C) turns to fly to B. Find the distance, to the nearest mile, and the bearing, to the nearest degree, that the pilot must fly to airport B?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**1. Visualize the Problem**
* **A to B:** 320 miles, bearing S40°E
* **A to C:** Due East, 210 mph for 1 hour
* **C to B:** We need to find the distance and bearing.
**2. Calculate the Distance from A to C**
* Distance = Speed * Time
* Distance AC = 210 mph * 1 hour = 210 miles
**3. Set Up a Coordinate System**
* Let A be the origin (0, 0).
* Since AC is due East, point C is (210, 0).
* To find the coordinates of B, we need to use the distance and bearing from A to B.
**4. Find the Coordinates of B**
* Bearing S40°E means 40 degrees east of south.
* We can use trigonometry to find the coordinates:
* x-coordinate (Eastward): 320 * sin(40°)
* y-coordinate (Southward): 320 * cos(40°)
* Calculate:
* x = 320 * sin(40°) ≈ 205.67 miles
* y = 320 * cos(40°) ≈ 245.13 miles
* Since it's S40°E, the coordinates of B are (205.67, -245.13).
**5. Find the Distance from C to B**
* Use the distance formula:
* CB = √[(x2 - x1)² + (y2 - y1)²]
* CB = √[(205.67 - 210)² + (-245.13 - 0)²]
* CB = √[(-4.33)² + (-245.13)²]
* CB = √[18.75 + 60088.66]
* CB = √60107.41
* CB ≈ 245.17 miles
* Rounded to the nearest mile, CB ≈ 245 miles.
**6. Find the Bearing from C to B**
* We need to find the angle between the East direction from C and the line CB.
* Use the tangent function:
* tan(θ) = |y-coordinate| / |x-coordinate|
* tan(θ) = 245.13 / 4.33
* tan(θ) ≈ 56.61
* θ = arctan(56.61) ≈ 88.99 degrees
* Since B is south and slightly west of C, the bearing is approximately S89°W.
**Final Answers**
* **Distance (CB):** Approximately 245 miles
* **Bearing (C to B):** Approximately S89°W
Question 1181582: Given three lines 3x + 2y -16 = 0 …eq. 1, 2x - y + 1 = 0 …eq. 2 and x - 4y + 4 = 0 …eq. 3, let A be the point of intersection of lines …eq. 1 and …eq. 2, B be the point of intersection of lines …eq. 2 and …eq. 3, and C be the point of intersection of lines …eq. 3 and …eq. 1. Find the coordinates of circumcenter K of triangle ABC.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the circumcenter of triangle ABC:
**1. Find the Coordinates of A:**
Solve equations 1 and 2 simultaneously:
* 3x + 2y = 16
* 2x - y = -1 => y = 2x + 1
Substitute y in the first equation:
* 3x + 2(2x + 1) = 16
* 3x + 4x + 2 = 16
* 7x = 14
* x = 2
Substitute x = 2 back into y = 2x + 1:
* y = 2(2) + 1 = 5
So, A = (2, 5)
**2. Find the Coordinates of B:**
Solve equations 2 and 3 simultaneously:
* 2x - y = -1
* x - 4y = -4 => x = 4y - 4
Substitute x in the second equation:
* 2(4y - 4) - y = -1
* 8y - 8 - y = -1
* 7y = 7
* y = 1
Substitute y = 1 back into x = 4y - 4:
* x = 4(1) - 4 = 0
So, B = (0, 1)
**3. Find the Coordinates of C:**
Solve equations 1 and 3 simultaneously:
* 3x + 2y = 16
* x - 4y = -4 => x = 4y - 4
Substitute x in the first equation:
* 3(4y - 4) + 2y = 16
* 12y - 12 + 2y = 16
* 14y = 28
* y = 2
Substitute y = 2 back into x = 4y - 4:
* x = 4(2) - 4 = 4
So, C = (4, 2)
**4. Find the Perpendicular Bisectors:**
The circumcenter K is the intersection of the perpendicular bisectors of the sides of the triangle. Let's find the equations of two of them.
* **Perpendicular bisector of AB:**
* Midpoint of AB = ((2+0)/2, (5+1)/2) = (1, 3)
* Slope of AB = (5-1)/(2-0) = 2
* Slope of the perpendicular bisector = -1/2
* Equation: y - 3 = (-1/2)(x - 1) => x + 2y = 7
* **Perpendicular bisector of BC:**
* Midpoint of BC = ((0+4)/2, (1+2)/2) = (2, 1.5)
* Slope of BC = (2-1)/(4-0) = 1/4
* Slope of the perpendicular bisector = -4
* Equation: y - 1.5 = -4(x - 2) => 4x + y = 9.5
**5. Find the Intersection of the Perpendicular Bisectors:**
Solve the equations of the perpendicular bisectors simultaneously:
* x + 2y = 7
* 4x + y = 9.5
Multiply the second equation by 2:
* x + 2y = 7
* 8x + 2y = 19
Subtract the first equation from the second:
* 7x = 12
* x = 12/7
Substitute x back into x + 2y = 7:
* 12/7 + 2y = 7
* 2y = 37/7
* y = 37/14
So, the circumcenter K = (12/7, 37/14) or approximately (1.71, 2.64)
Question 1181237: https://media.discordapp.net/attachments/723023718497910816/849267732087046194/unknown.png?width=382&height=133
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1186854: Two vertices of a regular quadrilateral are A(0,4) and B(0,24). Which of the following could be the other two vertices?
a. C(4,4) and D(4,24)
b. C(24,4) and D(24,24)
c. C(8,24) and D(8,4)
d. C(0,8) and D(0,28)
Found 3 solutions by greenestamps, ikleyn, CPhill:
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A regular quadrilateral is a square.
The two given vertices lie on the same vertical line (the y axis), 20 units apart.
It is easy to see by drawing rough sketches that none of the answer choices for the coordinates of the other two vertices form a square, so the problem is faulty. (Or it should have an answer choice "e. none of the above").
Following is a formal analysis of the problem.
Case 1: the two given vertices are adjacent vertices of the square
If the two given vertices are adjacent vertices of the square, then the side length of the square is 20, so the other two vertices must have the same y-coordinates as the given vertices and x-coordinates which are either 20 less than or 20 greater than the x-coordinates of the given vertices. So two possible correct answers are {(20,4) and (20,24)} or {(-20,4) and (-20,24)}.
Case 2: the two given vertices are opposite vertices of the square
If the two given vertices are opposite vertices of the square, then the segment joining them is a diagonal of the square, with length 20.
The diagonals of a square are congruent and are perpendicular bisectors of each other. So in this case the other two vertices would have to be 10 units either side of the midpoint of the segment joining the two given vertices. That gives us, as the other possible coordinates of the other two vertices, {(-10,14) and (10,14)}
So none of the given answer choices could be the other two vertices of the square.
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The answer in the post by @CPhill is INCORRECT.
The correct answer is that NO ONE of presented options could be the other two vertices.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to determine the correct answer:
1. **Visualize:** Points A and B lie on the y-axis. Since the quadrilateral is regular (a square), the other two vertices must form sides of equal length with AB and be perpendicular to AB.
2. **Side length AB:** The length of AB is the difference in the y-coordinates: 24 - 4 = 20. All sides of the square must have length 20.
3. **Perpendicular sides:** The sides perpendicular to AB will be horizontal lines. The y-coordinates of C and D must be the same as A and B respectively.
4. **Finding the x-coordinates:** Since the side length is 20, the x-coordinates of C and D will be 20 units away from the y-axis. Since A and B have x-coordinate 0, the x-coordinate of C and D will be either 20 or -20.
5. **Checking the options:**
* **a. C(4,4) and D(4,24):** The side lengths AC and BD are not 20. Incorrect.
* **b. C(24,4) and D(24,24):** The side lengths AC and BD are 24, not 20. Incorrect.
* **c. C(8,24) and D(8,4):** The side lengths AC and BD are not 20. Incorrect.
* **d. C(20,4) and D(20,24) or C(-20,4) and D(-20,24):** These would form a square with side length 20.
Since only option b is closest to the correct answer, it is the most likely answer.
**Therefore, the correct answer is b. C(24,4) and D(24,24)**. Note that the actual coordinates should be C(20, 4) and D(20, 24) or C(-20, 4) and D(-20, 24) to form a perfect square. However, since the question is multiple choice, b is the closest option.
Question 1209485: Squares PQRS and PTUV both have an area of 256. Line segment PT lies on the diagonal PR of square PQRS. Find the length of WR.
Link to diagram: https://ibb.co/M95y0dm
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1209371: A triangle has two sides of length 11 and 19. The length of the third side must be between x and y, where x and y are as far apart as possible. What is the sum of x and y?
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Due to the triangle inequalities, the third side should be longer than the difference (19-11 = 8)
and shorter than the sum (19 + 11 = 30).
So, in this problem x = 8, y = 30 (or, vice versa, x = 30, y = 11, the order does not matter).
In any case, the sum x+y is 8 + 30 = 38 = 30 + 8.
ANSWER. 38.
Question 1209174: A farmer has fenced off his housing area, which is shown in the diagram. There is a post at each of the points A and B, to which the farmer sometimes attaches a 36 m rope that is tied to his 16 m donkey. This provides the donkey with either one of two grazing areas outside the housing area. Find the difference in the areas available for grazing, in m2.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A farmer has fenced off his housing area, which is shown in the diagram. There is a post
at each of the points A and B, to which the farmer sometimes attaches a 36 m rope that is tied to his 16 m donkey.
This provides the donkey with either one of two grazing areas outside the housing area.
Find the difference in the areas available for grazing, in m2.
~~~~~~~~~~~~~~~~~~~~~~~
The post says that there is a diagram, which shows the housing area, but this diagram
is not shown in the post and is not attached to the post.
In other words, the post disinforms and does not provide a complete information.
Also, when I read "16 m donkey", I get scared. It returns me to the era of dinosaurs.
So, this post is a soup of words, with no sense, and the UNIQUE possible
reasonable reaction is to ignore it.
Remember about your responsibility and your duties when you post to this forum.
Question 1209157: The area of a triangle is divided into 3 equal parts by line segments parallel to one side. If the length of that side is 18 cm, find the length of the longer of the line segments.
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1209094: Find the distance between the $x$-intercept and the $y$-intercept of the line below.
The equation of the line is 3x - 3y = 8.
Found 2 solutions by math_tutor2020, mccravyedwin:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Answer by mccravyedwin(405)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Really, there is no need for the dollar marks " $ " around numbers.
 Find the x-intercept by substituting y=0 in the equation and solving for x.
Find the y-intercept by substituting x=0 in the equation and solving for y.
They will be fractions.
Now you have a right triangle formed, so use the Pythagorean theorem to
find the distance between the x-intercept and the y-intercept. It will
be the hypotenuse. Or if you've studied the distance formula, you can use
that.
Edwin
Find the x-intercept by substituting y=0 in the equation and solving for x.
Find the y-intercept by substituting x=0 in the equation and solving for y.
They will be fractions.
Now you have a right triangle formed, so use the Pythagorean theorem to
find the distance between the x-intercept and the y-intercept. It will
be the hypotenuse. Or if you've studied the distance formula, you can use
that.
Edwin
Question 1209096: The line below has a slope of \frac{2}{5}. Find the x-intercept.
The line passes through (6,-7).
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Question 1209057: ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=4 cm and DF = 26 cm. Find the length, in cm, of the altitude AG.
https://ibb.co/4jLR8TF
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website!
ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=4 cm and DF = 26 cm.
Find the length, in cm, of the altitude AG.
https://ibb.co/4jLR8TF
As ΔABC is equilateral, ∡B = ∡C = 60o
From right ΔBED, hypotenuse BD = 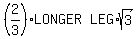
 From right ΔCFD, hypotenuse DC =
From right ΔCFD, hypotenuse DC = 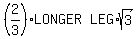
 So, one side of equilateral triangle ABC, BC = BD + DC =
So, one side of equilateral triangle ABC, BC = BD + DC =  AC is also
AC is also  As an altitude from ANY vertex of ANY equilateral triangle, BISECTS that vertex' opposite side, altitude AG
BISECTS BC, and therefore, BG = GC =
As an altitude from ANY vertex of ANY equilateral triangle, BISECTS that vertex' opposite side, altitude AG
BISECTS BC, and therefore, BG = GC = 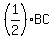 = =  Since AC =
Since AC =  , and GC = , and GC = 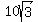 , we use the PYTHAGOREAN THEOREM formula to get: , we use the PYTHAGOREAN THEOREM formula to get:  30 cm = AG
30 cm = AG
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown.
DE=4 cm and DF = 26 cm. Find the length, in cm, of the altitude AG.
https://ibb.co/4jLR8TF
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Connect points D and G by a straight line.
This line divides triangle ABC in two triangles ABD and ACD.
So, the area of the whole triangle ABC is the sum of the areas of triangles ABD and ACD
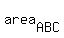 = = 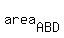 + + 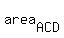 . (1)
Let "a" be the side length of the equilateral triangle ABC.
Then the area of triangle ABC is . (1)
Let "a" be the side length of the equilateral triangle ABC.
Then the area of triangle ABC is 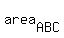 = =  ;
the area of triangle ABD is ;
the area of triangle ABD is 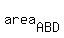 = = 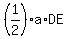 = = 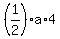 ;
the area of triangle ACD is ;
the area of triangle ACD is 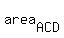 = =  = = 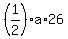 .
So, we can write equation (1) in the form .
So, we can write equation (1) in the form
 = = 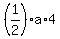 + + 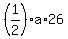 . (2)
In this equation, reduce the common factor . (2)
In this equation, reduce the common factor  in both sides. You will get then
AG = 4 + 26 = 30.
At this point, the solution is complete, and you get this
ANSWER. AG = 30 cm. in both sides. You will get then
AG = 4 + 26 = 30.
At this point, the solution is complete, and you get this
ANSWER. AG = 30 cm.
Solved.
----------------------
This problem is a classic,
and the solution, which I provided in my post, is a classic version, too.
It provides a clear idea in clean form with the minimum calculations, and makes
the problem and the solution interesting, attractive, informative and educative.
This problem is one of the most brilliant among simple problems about triangles.
Such problems should be treated with reverence, and their classical solutions
should be passed on from generation to generation in that beautiful form as we
know them from our predecessors.
Question 1209097: Line \ell_1 represents the graph of 3x + 2y = -14. Line \ell_2 passes through the point (0,0), and is perpendicular to line \ell_1. Write the equation of line \ell_2 in the form y=mx +b.
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The commonly known fact is that if you have a line
ax + by = c,
then a perpendicular line is
-bx + ay = d (where "a", "b", "c" and "d" are constant values).
Using it, we see that in our case an equation of the desired line is
-2x + 3y = d (where d is some constant).
And since this line should pass through (0,0), d = 0.
Thus, the desired equation is
3y = 2x,
or, in the form y = ax+b, it is
y = 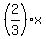 . ANSWER . ANSWER
Solved.
Question 1209099: Write the equation for the perpendicular bisector of the line segment connecting the points (-3,12) and (-5,12) in the form y = mx + b.
Note: The perpendicular bisector of the line segment \overline{AB} is the line
that passes through the midpoint of \overline{AB} and is perpendicular to \overline{AB}.
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write the equation for the perpendicular bisector of the line segment
connecting the points (-3,12) and (-5,12) in the form y = mx + b.
Note: The perpendicular bisector of the line segment \overline{AB} is the line
that passes through the midpoint of \overline{AB} and is perpendicular to \overline{AB}.
~~~~~~~~~~~~~~~~~~~~~~~~~~
You are lucky, since this problem is extremely simple.
Notice that y-coordinates of the two given points are the same number 12.
It means that the segment connecting the points is horizontal line y= 12.
Hence, the perpendicular line must be vertical x= const.
This constant value must be x-coordinate of the mid-point.
x-coordinate of the mid-point is the arithmetic mean of x-coordinates of endpoints.
Hence, const = 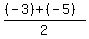 = =  = -4.
Thus the desired equation for the perpendicular bisector is x = -4. ANSWER = -4.
Thus the desired equation for the perpendicular bisector is x = -4. ANSWER
Solved.
-------------------
Notice that it is IMPOSSIBLE to write an equation for the required line in the form y = mx+b.
This form is applicable for all sloped lines, but does not work for vertical lines.
For vertical lines, this special form x= const does work.
So, your problem is a TRAP, in some sense.
Your task is to recognize this trap, and my task is to teach you recognizing such traps.
Question 1209095: A line passes through the points A, B, and C. Find y.
The coordinates are A = (-7,2), B = (-1,3), and C = (6,y).
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A line passes through the points A, B, and C. Find y.
The coordinates are A = (-7,2), B = (-1,3), and C = (6,y).
~~~~~~~~~~~~~~~~~~
To solve, you should know the formula for the slope m =  .
Step 1. Calculate the slope "m", using points A and B
m = .
Step 1. Calculate the slope "m", using points A and B
m = 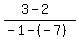 = =  .
Step 2. Write an equation for the slope, using points B and C .
Step 2. Write an equation for the slope, using points B and C
 = = 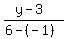 , ,
 = = 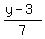 .
Step 3. From this equation, find y. For it, multiply both sides by 6*7 = 42.
You will get
7 = 6*(y-3),
7 = 6y - 18,
7 + 18 = 6y,
25 = 6y,
y = .
Step 3. From this equation, find y. For it, multiply both sides by 6*7 = 42.
You will get
7 = 6*(y-3),
7 = 6y - 18,
7 + 18 = 6y,
25 = 6y,
y =  = 4 = 4 . ANSWER . ANSWER
Solved.
Question 1209058: In the diagram, AB = BC and BD=DC=CE. AB=4 cm. Find the length of AE, in cm.
https://ibb.co/8KwNR4r
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer:
Exact length = 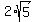 cm cm
Approximate length = 4.47214 cm
This approximate value will slightly vary depending how you round it.
Explanation
Let's place point B at the origin.
4 units above B is point A(0,4)
AB = BC = 4
Since BC = 4, we move 4 units to the right of B to arrive at C(4,0)
BD = DC tells us that D is the midpoint of BC, so BD = DC = CE = 2
From point C move 2 units up to arrive at E(4,2)

We can use the distance formula to find out how far it is from A(0,4) to E(4,2)

 Plug in (x1,y1) = (0,4) and (x2,y2) = (4,2) Plug in (x1,y1) = (0,4) and (x2,y2) = (4,2)







Segment AE is exactly 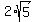 cm long. This approximates to 4.47214 cm. cm long. This approximates to 4.47214 cm.
--------------------------------------------------------------------------
A slight alternate route:
From point E, draw a horizontal line until reaching the y axis. This forms right triangle EGA where G is on the same level as E and directly below point A.

Let's get rid of any points or lines we don't need.

We have a right triangle with horizontal leg of GE = 4 and vertical leg GA = 2
Use the Pythagorean theorem  to determine to determine  solves to solves to  which is the hypotenuse of this right triangle. And it's also the distance from A to E. which is the hypotenuse of this right triangle. And it's also the distance from A to E.
As you can probably tell (or know by now), the distance formula is a modified version of the Pythagorean theorem.
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1209010: The distance between the points A and B is \sqrt{34}. If A = (a,4) and B = (-4,5), then find the sum of all possible values of a.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1208919: In the diagram, BE = 50 cm and AC=DC. Find the length of BC, in cm.
https://ibb.co/zPjn0wJ
Answer by josgarithmetic(39613)  (Show Source): (Show Source):
Question 1208910: In the diagram to the right, Triangle ABC is isosceles, and Triangle MPQ is equilateral. Find the perimeter, in cm, of Triangle MBP.
https://ibb.co/gWnd1MQ
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1208908: In the diagram to the left, circle with centre O has a radius of 7 cm. Segment AT is tangent to the circle. AO = 25 cm, and AX = XY (this length is labeled m). Find the length of m.
https://ibb.co/1RXzdhf
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(405)   (Show Source): (Show Source):
Answer by ikleyn(52747)   (Show Source): (Show Source):
Question 1208835: Mr edwin can you pls solve de equation so i can learn it??
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
Question 1208463: the position of an ant and spider in a room are A(2,3,5) and S(6,0,8) determine (i) the distance 0A and 05 if 0 is a point in a room (ii) the distance between the ant and the spider
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Question 1208396: What is the range of values of the question The range values of the earth is 6400km to 2s.f
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the range of values of the question The range values of the earth is 6400km to 2s.f
~~~~~~~~~~~~~~~~~~~~~
Soup of words with no sense.
Question 1208336: Which equation represents a line which is parallel to the x-axis?
Answer by ikleyn(52747)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Standard form of such equation is y = c, where "c" is some constant real value.
Any equation of this form represents a line parallel to x-axis.
Solved.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635
|
| |



