Question 222993: which of the four functions below has an inverse which is the same as the function itself?
A: f(x)=x-3
B: f(x)=1/2x
C: f(x)=-x-2
D: f(x)= the square root of x+2
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! In all these equations, let y = f(x).
To find the inverse function, solve for x and then replace y with x and x with y.
alternatively you can replace y with x and x with y first, and then solve for y.
Either way you'll get the same answer.
selection A
y = x+3
Solve for x to get:
x = y-3
Replace x with y and y with x to get:
y = x-3 which is the inverse function of y = x+3
Selection B
y = x/2
Solve for x to get:
x = 2y
Replace x with y and y with x to get:
y = 2x which is the inverse function of y = x/2
Selection C
y = -x-2
Solve for x to get:
x = -y-2
Replace x with y and y with x to get:
y = -x-2 which is the inverse function of y = -x-2
Selection D
y= sqrt(x+2)
Solve for x as follows:
Square both sides to get:
y^2 = x+2
Subtract 2 from both sides to get:
y^2-2 = x which is the same as:
x = y^2-2
Replace x with y and y with x to get:
y = x^2-2 which is the inverse function of y = sqrt(x+2)
Selection C inverse equation is the same as the original equation.
graph of this equation is shown below:

The line y = -x-2 is a reflection about the line y = x which is a definition of inverse function.
Take any point (x,y) on the line y = -x-2 above the line y = x. The opposite point (y,x) on the line y = -x-2 below the line will be the same distance from the line y = x.
example:
let x = -2
then y = -(-2)-2 = 2-2 = 0
your coordinate point is (-2,0).
now let x = 0
then y = 0-2 = -2
your coordinate point is (0,-2)
the point (-2,0) is a reflection of the point (0,-2) about the line y = x
to prove that the distance between these points and the line y = x is the same, we need to find the point of intersection between these two lines.
the point of intersection with the line y = x would be (-1,-1) as shown on the graph.
The distance between the point (-2,0) and (-1,-1) is given by the equation:
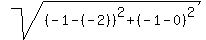 which equals which equals 
The distance between the point (0,-2) and (-1,-1) is given by the equation:
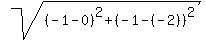 which equals which equals 
The point (-2,0) is a reflection of the point (0,-2) about the line y = x which is a requirement of inverse functions.
Selection C is your answer.
|
|
|