Question 125574This question is from textbook Mathematics 10
: 1/2(x-5)=x/4
I have tried this question so many ways, my head hurts. I can't figure it out! I only need one example and I will be able to complete my homework, unfortunately the text book does not give me an example. I have plans to go into school early if you can't help, but I thought I would give this a shot. I like to work things out on my own, but this is review from last year and after not seeing math problems for a year I'm struggling. Thanks
This question is from textbook Mathematics 10
Found 2 solutions by ankor@dixie-net.com, solver91311:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! The thing is, I'm not sure whether your problem is:  or or  , but I'm going to assume the former because the latter is trivial. , but I'm going to assume the former because the latter is trivial.
When dealing with rational functions, usually the best thing is to get everything on the left and leave 0 on the right to start:

Add 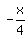 to both sides to both sides

Now you have the problem of adding two fractions with dissimilar denominators. You need to find a common denominator. Your denominators have a factor of 2 in common, so your LCD is 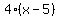 . So: . So:

Now that we have a common denominator, we can add the numerators, but first it will be convenient to distribute and remove the parentheses from the 2nd numerator. You can leave the denominator as it is for the time being.

Now, there is something to consider before you go any further. Is there a value of x that would make the denominator go to 0? The answer is yes, this function is undefined for x = 5, because that would give us a zero denominator. Therefore, if we arrive at a solution set that contains x = 5, we will have to exclude that solution.
The next thing to realize is that  if and only if if and only if  and and 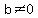 . So in order to solve this equation, we don't have to worry about the denominator (except to exclude 5 if it comes up as a solution) and all we have to do is set the numerator equal to zero and solve the quadratic. . So in order to solve this equation, we don't have to worry about the denominator (except to exclude 5 if it comes up as a solution) and all we have to do is set the numerator equal to zero and solve the quadratic.

Multiply by -1

This one doesn't factor neatly, so the best alternative is the quadratic formula:




We don't have to worry about excluding 5 because we got a conjugate pair of irrational roots.
Since root 33 is larger than 5, one of the roots is negative and the other is positive. We would then expect a graph of the original function to cross the x-axis once to the left of the y-axis, and once to the right of the y-axis. We would also expect to see a vertical asymptote at x = 5.
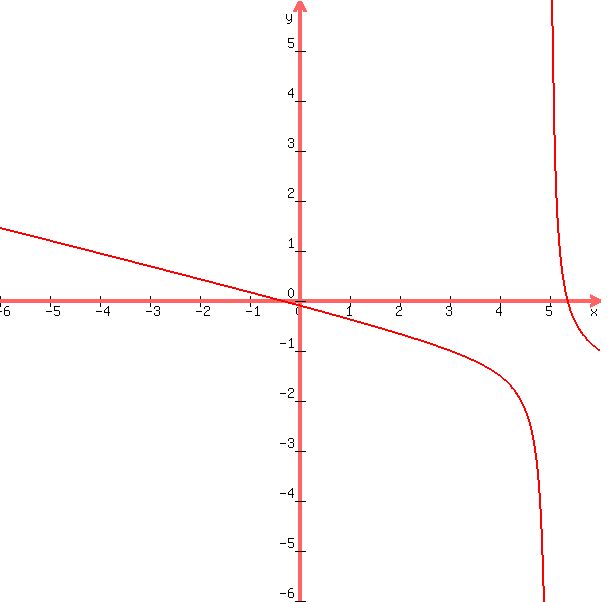
As advertised.
|
|
|