Question 1104382: if m - 1/m = 5; find:
(i) m^2 + 1/m^2
(ii) m^4 + 1/m^4
(iii) m^2 - 1/m^2
I solved the first two but I am unable to solve no. (iii).
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will solve (iii) only.
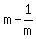 = 5 ====>
m^2 - 5m - 1 = 0 ====> (apply the quadratic formula) = 5 ====>
m^2 - 5m - 1 = 0 ====> (apply the quadratic formula)
 = =  = = 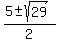 .
In other words, .
In other words, 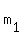 = = 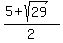 , ,  = = 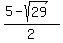 .
Notice that .
Notice that 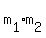 = -1.
You can check it by making direct calculations = -1.
You can check it by making direct calculations
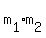 = = 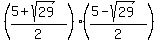 = = 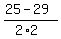 = = 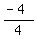 = -1,
or derive it from the Vieta's theorem.
Thus = -1,
or derive it from the Vieta's theorem.
Thus 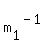 = =  = = 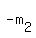 and and 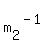 = = 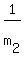 = = 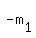 .
It implies .
It implies 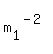 = = 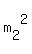 = = 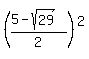 = = 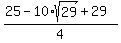 = = 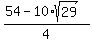 = = 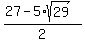 , and , and
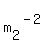 = = 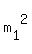 = = 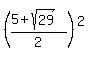 = = 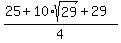 = = 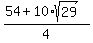 = = 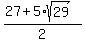 .
Thus you have .
Thus you have
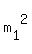 = = 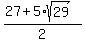 , , 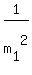 = = 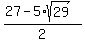 , which implies , which implies 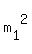 - - 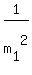 = = 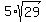 , and , and
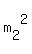 = = 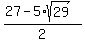 , , 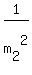 = = 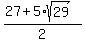 , which implies , which implies 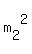 - - 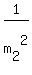 = = 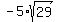 , ,
Answer. If  - -  = 5, then this equation has TWO solutions; correspondingly, "m" has TWO values; = 5, then this equation has TWO solutions; correspondingly, "m" has TWO values;
correspondingly, 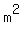 has TWO values, and, correspondingly, has TWO values, and, correspondingly, 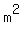 - - 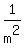 has two values +/- has two values +/- 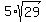 . .
Solved.
|
|
|