Question 108982: There was a party and everyone shook everyone's hands. There were 66 handshakes!! How many people were at the party???????????
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! There was a party and everyone shook everyone's hands. There were 66 handshakes!! How many people were at the party?
we know that:
with two people (x and y), there is 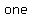 handshake; ( handshake; ( with with  ) )
with three people (x,y, and z), there are  handshakes; x with y and z, and y with z handshakes; x with y and z, and y with z
with four people (x, y, z, and e), there are 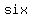 handshakes; x with y, z, and e, then y with z and e, then z with e handshakes; x with y, z, and e, then y with z and e, then z with e
In general:
with  people, the number of handshakes people, the number of handshakes 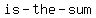 of the of the
first  consecutive numbers: consecutive numbers: 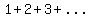
Since this  is is 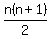 , ,
we need to solve the equation  ...multiply both sides by ...multiply both sides by  .=> .=>  ....=>... ....=>...
this is the quadratic equation 
use quadratic formula and solve for  : :

since  }, },  , and , and  , you will have: , you will have:




we need only positive root:



we obtain  as the answer and deduce that as the answer and deduce that 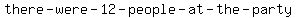 . .
|
|
|