Question 1073969: Hi I asked a question in this link but the person got it wrong, can someone try again please? Thank you.
https://www.algebra.com/tutors/students/your-answer.mpl?question=1073789
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! We sometimes use symbols that are difficult to interpret, or make mistakes while typing (or while thinking), but we try.
The function  , with all real numbers as its domain, , with all real numbers as its domain,  is not invertible, is not invertible,
because (like all quadratic functions) it has a vertical axis of symmetry.
That axis of symmetry is the line  : :  . .
By restricting the domain of the function
to a domain that does not include points on both sides of that axis,
we can make  invertible. invertible.
Defining the function only for a set of points with  , ,
or to a set of points with  , makes the function invertible. , makes the function invertible.
If we want to include the point  in the domain, in the domain,
we cannot include any point with 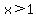 , ,
but we can include any point with  . .
The largest restricted domain that includes the point  , ,
but does not contain any point with 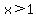 is is
all real  such that such that  . .
That can be expressed in interval notation as
  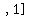 or or  . .
That is the largest interval that includes the point  , ,
where we can make  invertible. invertible.
That is the largest such interval that includes the point  . .
The equation for the axis of symmetry can be found by transforming the function, or by applying a formula.
With formulas:
All quadratic functions can be written in the form  , ,
for some constants 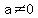 , ,  and and  . .
The axis of symmetry for such a function is the line 
 is a quadratic function with is a quadratic function with  and and  , ,
so its axis of symmetry is
 --> -->  ---> --->  . .
Transforming the function:
 or or 



The inverse for  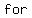   , , is is
 ---> --->  ---> --->  ---> --->  , ,
or   . .
Here are the graphs for  , , 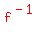 , and , and  , which is the line you flip , which is the line you flip  over to get over to get 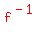 : :

|
|
|