Question 1044351: The sum of the reciprocals of two consecutive integers is equal to 11 times the reciprocal of the product of those integers.what are the two integers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's say that
 = one of the integers involved, with = one of the integers involved, with 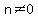 , so that the reciprocal of , so that the reciprocal of  exists. exists.
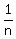 = the reciprocal of the integer above. = the reciprocal of the integer above.
For consecutive integers, let's say that
 = the other integer, also with = the other integer, also with 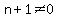 , so , so
 = the reciprocal of the "other integer" above. = the reciprocal of the "other integer" above.
So, 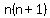 = the product of those integers. = the product of those integers.
Since neither  , nor , nor  is zero, is zero,
neither is their product: 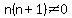 ,so the reciprocal exists. ,so the reciprocal exists.
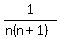 = the reciprocal of the product of those two consecutive integers. = the reciprocal of the product of those two consecutive integers.
What the problem says is that

That is the equation to simplify and solve.




Since  , we can multiply both sides of the equation times , we can multiply both sides of the equation times 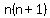 to get a simpler, equivalent equation. to get a simpler, equivalent equation.







The two integers are  and and  . .
|
|
|