|
Question 994271: The height of a projectile is modeled by equation y=-2x^2+38x+10, where x is time, in seconds, and y is height, in feet. During what interval of time to the nearest temth of a second is the projectile at least 125 feet above the ground?
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! y = -2x^2 + 38x +10
this is a parabola that curves downward, the x coordinate(time in seconds) for the maximum height is calculated using the following formula,
x = -b / 2a = -38 / (2*(-2)) = 9.5 seconds
now solve equation for x, given height of 125 feet
125 = -2x^2 + 38x +10
subtract 10 from both sides of =
-2x^2 + 38x = 115
divide both sides of = by -2
x^2 - 19x = -57.5
complete the square
x^2 - 19x + 90.25 = -57.5 + 90.25
(x - 9.5)^2 = 32.75
take square root of both sides of =
x - 9.5 = 5.722761571
x = 15.222761571 approx 15.2 seconds
15.2 seconds is on the right side of the parabola but we also want the left side as well
15.2 - 9.5 = 5.7, this tells us that 125 feet occurs 5.7 seconds after the maximum height at 9.5 seconds, to find the x coordinate for the left side of the parabola we calculate 9.5 - 5.7 = 3.8 seconds, therefore the interval of time the projectile is at least 125 feet above the ground is
****************************************************************************
[3.8, 15.2]
****************************************************************************
here is a graph of the equation to help visualize the answer
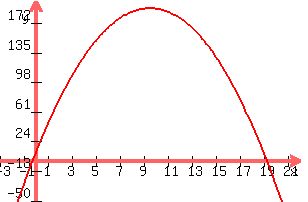
|
|
|
| |