Question 988807: Solve for x in the inequality:
-1 is less than (x+2)/(x-3)
Any tips, tricks, advice for other inequality problems is greatly appreciated as well as help with this problem! Thank you in advance!
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Solve for x in the inequality:
-1 is less than (x+2)/(x-3)
Any tips, tricks, advice for other inequality problems is greatly appreciated as well as help with this problem! Thank you in advance!
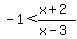 , with , with 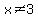 as this would make the denominator 0, and therefore, an UNDEFINED inequality as this would make the denominator 0, and therefore, an UNDEFINED inequality
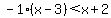 ----- Multiplying both sides by LCD, x - 3 ----- Multiplying both sides by LCD, x - 3
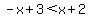
 -------- Subtracting 3 from both sides -------- Subtracting 3 from both sides
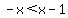
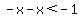 --------- Subtracting x from both sides --------- Subtracting x from both sides
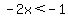
 -------- Inequality sign changes when dividing by a negative value -------- Inequality sign changes when dividing by a negative value
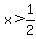
Now, we have the CRITICAL VALUES: 
This means that we will have THREE (3) TEST-INTERVALS to determine whether or not values
in the intervals SATISFY the ORIGINAL inequality: 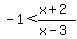 . These TEST INTERVALS are: . These TEST INTERVALS are:
1) 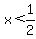
2) 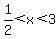 , and , and
3) 
Testing 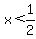 with test value: with test value:  , , 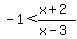 becomes: becomes: 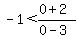
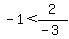
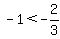
As the above is TRUE, the test-interval: 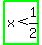 IS a solution IS a solution
Testing 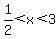 with test value: with test value:  , , 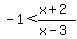 becomes: becomes: 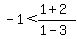


As the above is FALSE, the test-interval: 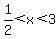 IS NOT a solution IS NOT a solution
Testing  with test value: with test value:  , , 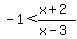 becomes: becomes: 
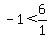
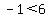
As the above is TRUE, the test-interval: 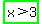 IS a solution IS a solution
In interval notation, this is: (- oo, ½) ᑌ (3, oo) , or (   ) ᑌ ( ) ᑌ (   ) )
|
|
|