Question 9496: Why does an inequality reverse when you multiply or divide an inequality by a negative number?
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Take for example -4 < 6, which you know is a true statement.
Now, multiply both sides by 3:
3(-4) < 3(6)
-12 < 18 This is still true!
This is just one example, but for ANY other example, you will find that thit is true. It illustrates the concept that the inequality stays the SAME when multiplying or dividing by a POSITIVE number.
Now take -4 < 6, and multiply both sides by -2:
-4< 6
-2(-4)
8 > -12
Did you see what happened? When you multiplied both sides by a NEGATIVE number, what WAS negative became positive, and what WAS positive became negative! Everything that was larger became small, and what was smaller became large. Everything REVERSED.
The same thing happens when you divide both sides by a NEGATIVE! What WAS positive becmes negative, and what was negative becomes positive. Everything reverses:
-4 < 6
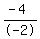 ?? ?? 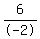
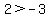
When you multiply or divide both sides of an inequality by a NEGATIVE number, you must REVERSE the direction of the inequality!
R^2 at SCC
|
|
|