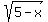

 Get 0 on the right.
Get 0 on the right.
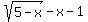

 In order for
In order for 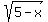 to be a real number we require
to be a real number we require
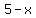




 which is the same as
which is the same as


 So 5 is a critical number, since no value of x
can be greater than 5
Next we look for critical numbers of
So 5 is a critical number, since no value of x
can be greater than 5
Next we look for critical numbers of
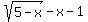

 By solving
By solving 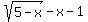


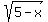


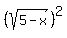


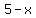

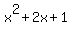


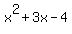


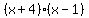 x+4=0; x-1=0
x=-4; x=1
So there are two more critical numbers
We plot the three critical numbers on a number line:
----------o--------------o-----------o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
We test a value in each of the three regions
For the leftmost region, we test x=-5 in
x+4=0; x-1=0
x=-4; x=1
So there are two more critical numbers
We plot the three critical numbers on a number line:
----------o--------------o-----------o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
We test a value in each of the three regions
For the leftmost region, we test x=-5 in
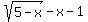


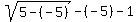


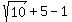




 The left side is a positive number, so that is false.
So the left region is not part of the solution:
----------o--------------o-----------o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
For the middle region, we test x=0 in
The left side is a positive number, so that is false.
So the left region is not part of the solution:
----------o--------------o-----------o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
For the middle region, we test x=0 in
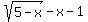







 The left side is a positive number, so that is false.
So the middle region is also not part of the solution:
----------o--------------o-----------o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
For the righmost region, we test x=2 in
The left side is a positive number, so that is false.
So the middle region is also not part of the solution:
----------o--------------o-----------o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
For the righmost region, we test x=2 in
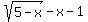





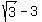

 The left side is a negative number, so that is true.
So the rightmost region is part of the solution,
so we shade that interval:
----------o--------------o===========o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Finally we test the critical numbers themselves to
see if they are solutions;
We test critical number -4 in
The left side is a negative number, so that is true.
So the rightmost region is part of the solution,
so we shade that interval:
----------o--------------o===========o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Finally we test the critical numbers themselves to
see if they are solutions;
We test critical number -4 in
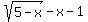


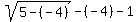


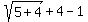


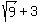


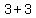




 That's false so critical number -4 is not a solution.
So we erase the open circle at -4:
-------------------------o===========o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
We test critical number 1 in
That's false so critical number -4 is not a solution.
So we erase the open circle at -4:
-------------------------o===========o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
We test critical number 1 in
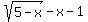





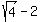


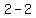




 That's false so critical number 1 is not a solution.
-------------------------o===========o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
We test critical number 5 in
That's false so critical number 1 is not a solution.
-------------------------o===========o
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
We test critical number 5 in
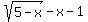


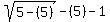


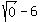




 That's true so 5 is a solution.
So we darken it:
-------------------------o===========●
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
So the solution is
1 < x ≤ 5
That can be written in interval notation as (1,5]
Edwin
That's true so 5 is a solution.
So we darken it:
-------------------------o===========●
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
So the solution is
1 < x ≤ 5
That can be written in interval notation as (1,5]
Edwin