Question 872665: Hello, I have a homework about inequalities:word problems.
The question states:
"For each of the following, a) choose a variable to represent the number indicated in parentheses. b) use the variable to write an inequality based on the given information, do not solve."
The exercise:
12. If a motorist drove 10 mi/h faster, then he would travel farther in 3 h than he does in 4 h at (his present speed).
Thank you, and please explain to me how it is solved, that would help me a lot.
{P.S. any help would be greatly appreciated.}
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = his present speed, in mi/h = his present speed, in mi/h
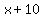 = a speed (in mi/h) 10 mi/h faster than his present speed = a speed (in mi/h) 10 mi/h faster than his present speed
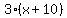 = distance he would travel in 3 hours, driving 10 mi/h faster than his present speed = distance he would travel in 3 hours, driving 10 mi/h faster than his present speed
 = distance he would travel in 4 hours, driving at his present speed = distance he would travel in 4 hours, driving at his present speed
The problem says that 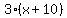 is a greater distance than is a greater distance than  . .
We write that as
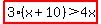
NOTE:
The part above answers "write an inequality based on the given information, do not solve."
If you want to know how to solve that inequality, here it goes
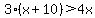
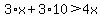
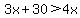
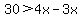
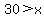 or or 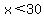
Reality check:
Does it make sense?
If he was driving at 30 mi/h, in 4 hours he would travel
(30 mi/h)(4 h) = 120 mi
Going 10 mi/h faster, at 30 mi/h + 10 mi/h = 40 mi/h,
in 3 hours he would travel the same distance
(40 mi/h)(3 h) = 120 mi.
However, if he is driving slower, for example at 29 mi/h,
in 4 hours he would travel
(29 mi/h)(4 h) = 116 mi.
Going 10 mi/h faster, at 29 mi/h + 10 mi/h = 39 mi/h,
in 3 hours, the distance he would travel is
(39 mi/h)(3 h) = 117 mi,
so driving 10 mi/h faster, he would indeed travel farther in 3 h.
The conclusion is
if you are driving slow, increasing your speed by 10 miles per hour would help.
If you are already going at a good speed, you do not gain that much by driving 10 miles per hour faster.
We sort of knew that, didn't we?
|
|
|