(-6, 8)
That means this interval:
-------(=========================================)------
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
locate the mid point of this interval by averaging -6 and 8
 So 1 in the exact middle of that interval. I'll mark it M
-------(====================M====================)------
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
The interval (-6,8) contains all the points up to 8-1 or 7 units
to the right of M=1 and all the points up to 1-(-6) or 7 units to
the left of M=1.
Let x be any point on the interval.
If x is to the right of 1, if you subtract 1 from it, x-1, you
will always get a number between 0 and 6.
If x is to the left of 1, if you subtract 1 from it, x-1, you
will always get a number between -6 and 0.
So you combine the two preceding statements by saying:
If x is on the interval, regarless of whether it's to the right or left
of -1, if you subtract 1 from it, x-1 AND TAKE THE ABSOLUTE VALUE of it,
|x-1|, it will always be between 0 and 6, so
|x-1|<6 is the answer.
If you want a formula,
(a,b) is equivalent to
So 1 in the exact middle of that interval. I'll mark it M
-------(====================M====================)------
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
The interval (-6,8) contains all the points up to 8-1 or 7 units
to the right of M=1 and all the points up to 1-(-6) or 7 units to
the left of M=1.
Let x be any point on the interval.
If x is to the right of 1, if you subtract 1 from it, x-1, you
will always get a number between 0 and 6.
If x is to the left of 1, if you subtract 1 from it, x-1, you
will always get a number between -6 and 0.
So you combine the two preceding statements by saying:
If x is on the interval, regarless of whether it's to the right or left
of -1, if you subtract 1 from it, x-1 AND TAKE THE ABSOLUTE VALUE of it,
|x-1|, it will always be between 0 and 6, so
|x-1|<6 is the answer.
If you want a formula,
(a,b) is equivalent to 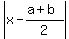

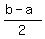 If you want to go the other way,
|x-h| < k (if k > 0) is equivalent to h-k < x < h+k
--------------------------------------------------
Using "oo" for "infinity",
(-oo,a) U (b,oo) (if a < b) is equivalent to
If you want to go the other way,
|x-h| < k (if k > 0) is equivalent to h-k < x < h+k
--------------------------------------------------
Using "oo" for "infinity",
(-oo,a) U (b,oo) (if a < b) is equivalent to 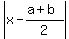

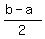 |x-h| > k (if k > 0), is equivalent to " x < h-k OR x > h+k ".
Edwin
|x-h| > k (if k > 0), is equivalent to " x < h-k OR x > h+k ".
Edwin