SOLUTION: Suppose a, b, c are all real numbers such that a+b+c > 0; abc > 0 and ab+bc+ac > 0: Show that a, b, c are all positive.

Algebra ->  Inequalities -> SOLUTION: Suppose a, b, c are all real numbers such that a+b+c > 0; abc > 0 and ab+bc+ac > 0: Show that a, b, c are all positive.      Log On


   

Question 825994: Suppose a, b, c are all real numbers such that a+b+c > 0; abc > 0 and ab+bc+ac > 0:
Show that a, b, c are all positive.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
(1)  a+b+c > 0; 
(2)  abc > 0 
(3)  ab+bc+ac > 0

Prove a>0, b>0, c>0

Since abc > 0, none are 0, and either all three are positive
or one of them is positive and the other two are negative.

If all three are positive the theorem is proved.

For contradiction assume a<0, b<0 and c>0

Then let -a=x>0, and -b=y>0
Substitute a=-x and b=-y in (3)

    (-x)(-y)+(-y)c+(-x)c > 0     [All the letters are now positive]
                xy-cy-cx > 0
(4)                   xy > cx+cy

Substitute a=-x and b=-y in (1)

                  -x-y+c > 0
                       c > x+y

Divide through by c
                      1 > 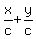x%2Fc%2By%2Fc

Both x%2Fc and y%2Fc are < 1 since both are positive,
i.e., they are positive proper fractions.

Therefore  x+y > expr%28x%2Fc%29%2Ay, for certainly the sum of x and y
is greater than only a fraction of y.

Multiply through by c

         cx+cy > xy

That contradicts (4).

The three given inequalities are symmetrical in a,b, and c,

so it's also a contradiction if a<0, b>0 and c<0, 
and if a<0, b>0 and c<0.

So all three a,b, and c are positive.

Edwin