|
Question 717810: Hi
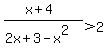
Thanks!
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 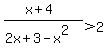
The first thing we want to do is eliminate the fraction. This will require that we multiply each side by 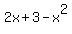 . After multiplying by . After multiplying by 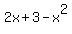 the left side will be (x+4) and the right side will be the left side will be (x+4) and the right side will be 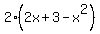
The problem is that it makes a difference whether 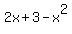 is positive or negative. If it is negative then we must reverse the inequality. Not knowing yet what value(s) x may have, we do not know right now if is positive or negative. If it is negative then we must reverse the inequality. Not knowing yet what value(s) x may have, we do not know right now if 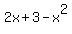 is positive or negative. So what we have to do is handle both situations. If is positive or negative. So what we have to do is handle both situations. If 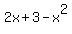 is positive then we don't reverse the inequality and if it is negative we do. The mathematical expressions that express this are: is positive then we don't reverse the inequality and if it is negative we do. The mathematical expressions that express this are:
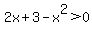 (positive) and (positive) and 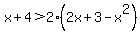 or or 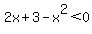 (negative) and (negative) and 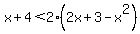
Simplifying the 2nd and 4th inequalities and putting all of them in standard ax+by+c form:
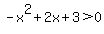 and and  or or 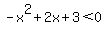 and and 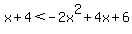
Now we start solving these inequalities. Solving quadratic inequalities is similar to solving quadratic equations. First we want one side to be zero. The 1st and 3rd inequalities already have a zero on one side. Making one side of the 2nd and 4th inequalities be zero:
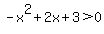 and and 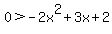 or or 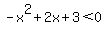 and and 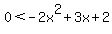
Next we factor. I'm going to do this one inequality at a time.
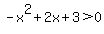
Factoring this will be easier if the leading coefficient is positive. So I will factor out -1. (We could multiply both sides by -1, too, if we remember to reverse the inequality.)
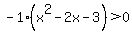
Factoring the trinomial:
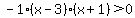
This is where solving quadratic inequalities becomes different from equations. With equations we would use the Zero Product Property next. But this property applies to products that are equal to zero. With an inequality we must do something different. What we have is a product of three factors that is greater than zero. Another way to say this is that we have a product of three factors that is positive. We should know that the product of three factors will be positive only if all three factors are positive or if two factors are negative and one of them is positive. One of our factors is -1 so we cannot get three positive factors. We must have two negative factors (the -1 being one of them) and the other factor must be positive.
But which one is going to be the positive one? Or could it be either? The answer is: (x+1) has to be the positive one. Why? Well no matter what number x might be, doesn't x+1 have to be greater than x-3? And since any positive number is greater than any negative number, x+1 must be the positive one. So
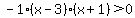
"boils down" to:
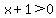 and and 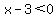
Solving these we get:
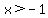 and and 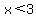
Skipping to
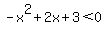
because it is so similar to the one we just did...
It factors the same way:
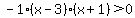
But this time we have a product of three factors that is negative. The only way this can be is if all three factors are negative or two of them are positive and one of them negative. Since we still have one factor, -1, that is negative no matter what and since both the possibilities include a negative factor, we have to handle both possibilities.
For all three negative we just have to have x+1 be negative. Why? Because if the larger factor, x+1, is negative, doesn't the smaller factor, x-3, end up being negative, too? So "all three factors" are negative boils down to:
x+1 < 0
For two positives and a negative, the -1 has to be the negative one. So we want both of the other factors to be positive. For this we just need x-3 to be positive. This is so because if the smaller factor, x-3, is positive, doesn't a larger factor, x+1, have to be positive, too? So two positives and one negative boils down to:
x-3 > 0
Altogether,
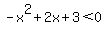
becomes:
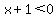 or or 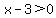
Solving these we get:
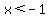 or or 
The logic for the remaining inequalities is the same as what we have used so far. So I am going to speed up.
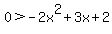

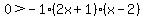
A product that is negative. (Always read inequalities from where the variable is. In this case, from right to left. And from right to left this is a "less than".) So like above, all three factors must be negative or two of them positive and the third is negative. This time, however, we do not know which factor is the larger factor. So we solve for both possibilities.
All three negative:
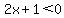 and and 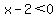
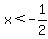 and and 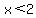
which boils down to just
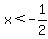
because if x is less than -1/2 doesn't it have to be less than 2, also? (But not the other way around.)
Two positive and one negative. With the -1 being the negative one, the others must be positive:
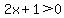 and and 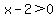
 and and 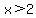
which boils down to just
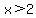
because if x is greater than 2 it must automatically be greater than -1/2 (but not the other way around). So the solution to
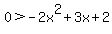
is
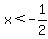 or or 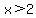
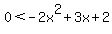
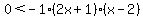
A product that is positive. With the negative factor of -1, this can happen only if one of the other factors is positive and the third one is negative:
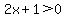 and and 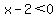 or or 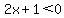 and and 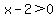
Solving these we get:
 and and 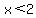 or or 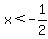 and and 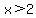
The last pair is impossible. It is impossible for x to be less than -1/2 and greater than 2 at the same time. So the solution to
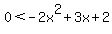
is
 and and 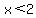
Now that we have the four inequalities of
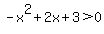 and and 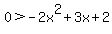 or or 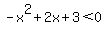 and and 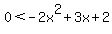
solved, let's replace each one with the solution we found:
(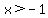 and and 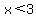 ) and ( ) and (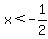 or or 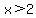 ) or ( ) or (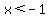 or or  ) and ( ) and ( and and 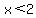 ) )
Now we simplify these. The "or" in the middle is the last thing to figure out. We simply each half as much as possible first.
The first half: (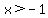 and and 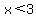 ) and ( ) and (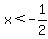
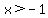 and and 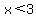 tells us that x must be between -1 and 3. tells us that x must be between -1 and 3. 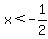 or or 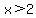 tells us that x must either be below -1/2 or larger than 2. The "and" between them tells us that both must be true. This means x must either be between -1 and -1/2 or between 2 and 3: tells us that x must either be below -1/2 or larger than 2. The "and" between them tells us that both must be true. This means x must either be between -1 and -1/2 or between 2 and 3:
(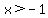 and and 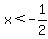 ) or ) or 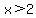 and and 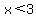
(If you have trouble seeing this then graph each inequality on a number line.)
The second half: (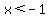 or or  ) and ( ) and ( and and 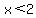 ) )
The first part, (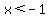 or or  ) says must must be less than -1 or greater than 3. The second part tells us that x must be between -1/2 and 2. The "and" between them says x must fit both parts. There are no such numbers. If x is less than -1 it is not between -1 and 2 and if x is greater than 3 it cannot be between -1/2 and 2. So there is no solution for the second half. ) says must must be less than -1 or greater than 3. The second part tells us that x must be between -1/2 and 2. The "and" between them says x must fit both parts. There are no such numbers. If x is less than -1 it is not between -1 and 2 and if x is greater than 3 it cannot be between -1/2 and 2. So there is no solution for the second half.
With no solution to the second half, the solution for the first half:
(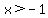 and and 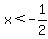 ) or ( ) or (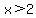 and and 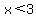 ) )
becomes the solution to:
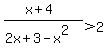
|
|
|
| |