Not "formulas", principles:
-4(t+6)-(t+1) = 2
Use the distributive principle to remove the
first set of parentheses. Multiply the -4 by
both the t and the 6 and get -4t-24 instead of
the -4(t+6), so we write this:
-4t-24-(t+1) = 2
To remove the next set of parentheses we first
put a 1 before the parentheses:
-4t-24-1(t+1) = 2
Use the distributive principle to remove the
first set of principle. Multiply the -1 by
both the t and the 1 and get -t-1 instead of
the -1(t+1), so we write this:
-4t-24-1t-1 = 2
Now we collect like terms. The -4t and the -1t
combine to give -5t. The -24 and the -1 gives
-25. So we have this:
-5t-25 = 2
Now we need to have the letter term -5t only on the
left side, so we must get rid of the -25 by using
the principle of adding the same number to both
-25 to both sides, so we add +25 to both sides
-5t-25+25 = 2+25
The -25 and the +25 cancel out on the left. The 2+25
on the right becomes 27
-5t = 27
Then we use the principle of dividing both sides by
the coefficient of t, which is -5, so as to leave
only the t
= 
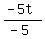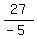t = 
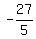You can leave it like that or divide it out and get
t = -5.4
Edwin
