SOLUTION: The solution to {{{ x^2 - x - 6 > 0 }}} is A. -3<x<2 B. x<-3 or x>2 C. -2<x<3 D. x<-2 or x>3 E. x>3

Algebra ->  Inequalities -> SOLUTION: The solution to {{{ x^2 - x - 6 > 0 }}} is A. -3<x<2 B. x<-3 or x>2 C. -2<x<3 D. x<-2 or x>3 E. x>3       Log On


   

Question 628401: The solution to +x%5E2+-+x+-+6+%3E+0+ is
A. -3 B. x<-3 or x>2
C. -2 D. x<-2 or x>3
E. x>3
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
+x%5E2+-+x+-+6+%3E+0+
With a quadratic inequality, just like a quadratic equation, you want one side to be a zero and then you factor the other side.

We already have a zero on one side so we can go straight to factoring. The left side factors fairly easily:
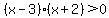
%28x-3%29%28x%2B2%29+%3E+0

With a quadratic equation the next step would be to use the Zero Product Property. With this inequality this product is specifically not a zero so we cannot use the property here. The next step is based on some logic:
  • The inequality says a product is greater than zero. Another way to say this is that the product is positive.
  • We have a product of two factor that is positive. How does this happen? There are only two ways you can multiply two numbers and get a positive result:
    • Multiplying two positive numbers; or
    • Multiplying two negative numbers.
The next step then is to translate "the two factors are positive or the two factors are negative" into a mathematical expression. "The two factors are positive" translates into:
(x-3 > 0 and x+2 > 0}
"The two factors are negative" translates into:
(x-3 < 0 and x+2 < 0}
This makes "the two factors are positive or the two factors are negative" translate into:
(x-3 > 0 and x+2 > 0} or (x-3 < 0 and x+2 < 0}

We could go ahead and solve this. But I's like to take a moment to explain how we can make this easier on ourselves by using a little extra logic. If any of the following does not make sense then just skip it and solve the above,

No matter what number x might be, can you agree that x+2 will work out to be a larger number than x-3? So x+2 will always be the larger factor. And if you want both factors to be positive, won't they both be positive if the smaller one is positive? So for both factors to be positive, all that needs to be true is: x-3 > 0.

We can use similar logic on the "both factors are negative". If the larger factor, x+2, is negative, wouldn't the smaller factor, x-3, also have to be negative? So to make both factors negative we we really need is:
x+2 < 0

So instead of solving
(x-3 > 0 and x+2 > 0} or (x-3 < 0 and x+2 < 0}
we could save ourselves some work (and possible confusion) by just solving:
(x-3 > 0} or (x+2 < 0}

Solving each of the above we get:
(x > 3) or (x < -2)
This is answer "D".