SOLUTION: Find the no. of integral solutions of: xy=2x-y i tried using the AM-GM inequality but i didnt get the solution to this.how should i start?

Algebra ->  Inequalities -> SOLUTION: Find the no. of integral solutions of: xy=2x-y i tried using the AM-GM inequality but i didnt get the solution to this.how should i start?       Log On


   

Question 570274: Find the no. of integral solutions of:
xy=2x-y
i tried using the AM-GM inequality but i didnt get the solution to this.how should i start?
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
      xy = 2x - y
  xy + y = 2x
y(x + 1) = 2x
       y = 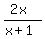%282x%29%2F%28x%2B1%29

The graph of that has vertical asymptote x=-1 and horizontal asymptote y=2.
We plot that graph:



The only possibility of y having an integral value when x has an integral
value, is for integral values of x when y is at least 1 unit away from
its horizontal asymptote y=2, and that is when

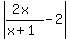
abs%28%282x%29%2F%28x%2B1%29+-+2%29 %22%22%3E=%22%22 1

By ordinary methods of college algebra, that has solution 

[-3,-1)U(-1,1]

So we only need to try x-values in that region

which are -3, -2, 0, and 1 

Substituting those in

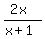y = %282x%29%2F%28x%2B1%29

we find the only four integral solutions: 

(-3,3),(-2,4),(0,0), (1,1).

So the number of integral solutions is 4.

Edwin