|
Question 476572: its all about non linear inequalities. (x-5)(x-4) is greater than or equal to 0.
Found 3 solutions by Theo, ikleyn, AnlytcPhil:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! easiest way to answer this is to graph it.
that's if you have the graphing software that makes it easy.
from the graph, it looks like this equation will be less than 0 between 4 and 5.
that stands to reason.
since this is a quadratic equation that has already been solved for the roots, it should be easy to determine what points in this equation are above 0 or below 0 or at 0.
the equation you have to work with is:
(x-5)*(x-4) = 0
by setting the expression equal to 0, you are looking for the roots.
the roots becomes:
x = 4 and x = 5
those are the zero points of the graph.
you multiply the factors together to get the original quadratic equation that gave you (x-5)*(x-4.
(x-5)*(x-4) = x^2 - 4x -5x + 20
combine like terms and you get:
x^2 - 9x + 20
if you set this equal to 0, then it becomes the standard form of the quadratic equation.
you get x^2 - 9x + 20 = 0
the standard form of the quadratic equation is ax^2 + bx + c = 0
this makes:
a = 1
b = -9
c = 20
the min/max point of the quadratic equation is given by the equation:
x = -b/2a
this becomes:
x = -(-9)/2) which becomes:
x = 4.5
That's the x value of the min/max point.
the y value of the min/max point is given by:
y = f(4.5)
you replace x with 4.5 in the equation and you get:
y = x^2 -9x + 20 which becomes:
y = (4.5)^2 -9*4.5 + 20 which becomes:
y = -.-025
your min/max point is at the (x,y) coordinates of (4.5,-.025).
now you want to determine whether this is a min point or a max point.
this is because you didn't see the graph i just showed you above.
you haven't even drawn the graph yet.
you're working just from the equation.
you look at the exponent of the x^2 term.
if it is positive then the graph points down and opens up.
if it is negative then the graph points up and opens down.
if the graph points down, then the min/max point is a min point.
if the graph points up, then the min/max point is a max point.
the graph is pointing down because the coefficient of the x^2 term is positive.
that would be the a in ax^2 which was equal to 1.
so your graph is point down.
the roots of the eqution are at x = 4 and x = 5
the min point is negative.
it will stay negative between the roots and it will be positive outside of the roots.
your equation is therefore >= 0 when:
x < 4 or x > 5
Answer by ikleyn(53028)  (Show Source):
You can put this solution on YOUR website! .
its all about non linear inequalities. (x-5)(x-4) is greater than or equal to 0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The methods Theo uses to teach students in his posts very often
are monstrously verbose, and needlessly long.
The true Math explanations are usually much shorter, much more straightforward,
much clearer, and more instructive.
So, they want you solve inequality (x-5)*(x-4) >= 0.
In this problem the function is presented as the product of two linear binomials, (x-5) and (x-4).
In order for the product of these two binomials would be non-negative, the factors/binomials
should be of the same sign or zero.
First factor, (x-5) is negative or zero in the area x <= 5 and non-negative or zero in the area x >= 5.
Second factor, (x-4) is negative or zero in the area x <= 4 and non-negative or zero in the area x >= 4.
Thus we see that both factors are negative or zero in the domain x <= 4,
and both factors are non-negative in the domain x >= 5.
Thus the solution set is the union of two semi-infinite intervals x <= 4 and x >= 5.
At this point, the solution is fully complete.
ANSWER. The solution is the set x <= 4 or x >= 5.
i.e. the area out of the interval between the roots of the function (but the solution set includes the roots).
To make sure that the solution is correct, you may plot the function. See this plot below.
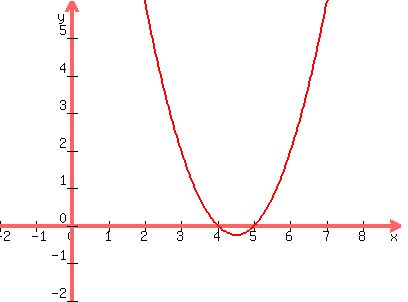Plot y = (x-5)*(x-4)
The function is a parabola opened upward. Its branches are in the upper (non-negative) half-plane out the interval
on x-axis between x-intercepts, but including the x-intercepts.
The part of the parabola between the roots is in the lover (negative) half-plane.
So, this figure confirms the logical reasoning in algebraic solution.
By the way, the answer in the post by @Theo, which is given as x < 4, x > 5,
is INCORRECT: it excludes the roots of the function.
Actually, the roots must be included.
///////////////////////////////////////////////
Couple of words about evolution of online solutions in the internet.
The era of online solutions and corresponding online websites started somewhere about the year ~ 2000.
First years it was at the mostly amateur level, but starting from the year ~ 2005, it transformed into
a commercial enterprise.
The flow of online Math problems and online solutions was huge, and practically nobody tracked
the quality of the solutions, as well practically nobody cared about it, because the major goal
was to capture territory.
Due to this reason, good and correct solutions were placed side by side with unprofessional posts.
This development continued till approximately the year 2024, when the Artificial Intelligence came.
The audience of users and readers grew from thousands to millions.
But the base of solved problems for Artificial Intelligence was half of professional posts
and half of unprofessional quality. So, the tone and the quality of many solutions produced by AI,
were often below commonly accepted standards both in Math and in Math education.
This situation was heavily criticized by the community, and for this reason, starting from August 2025,
the situations began to improve — the tone of many solutions changed; they are becoming increasingly acceptable.
And I'm proud to be contributing to improving the quality of online solutions.
Answer by AnlytcPhil(1810)  (Show Source):
|
|
|
| |
