Question 462450: find solution set of (3x+2)^100(5-x)^99/(2x-7)^101<=0
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The inequality is in standard form already (i.e., one side of the inequality is equal to zero).
The critical numbers are:
-2/3, 7/2, and 5.
( , -2/3): , -2/3): 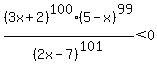 . (Choose test number x = -1.) . (Choose test number x = -1.)
( -2/3, 7/2): 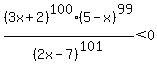 . (Choose test number x = 0). . (Choose test number x = 0).
(7/2, 5): 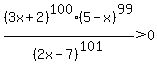 . (Choose test number x = 4.) . (Choose test number x = 4.)
(5,  ): ): 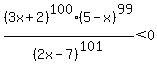 . (Choose test number x = 6.) . (Choose test number x = 6.)
The critical numbers -2/3 and 5 also satisfy the inequality, but not 7/2. Hence the solution set is the union
( , 7/2) U [5, , 7/2) U [5,  ). ).
|
|
|