|
Question 426938: A little help please?!
Find the system of inequalities whose feasible region is the interior of the rectangle with vertices (corner points) of (-3, 4); (5, 4); (5, -1); (-3, -1)
I have NO idea??
Thank you in advance!! :)
Answer by Theo(13342)   (Show Source): (Show Source):
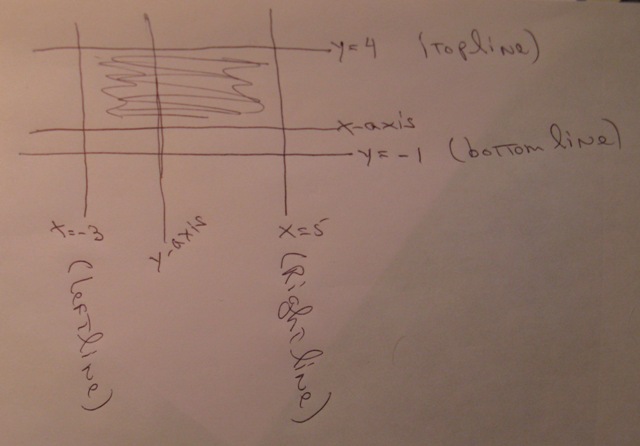
You can put this solution on YOUR website! you need to find the equation of the lines that make up the sides of this rectangle.
from the looks of your points, you have a vertical line that can be created between the points of (-3,4) and (-3,-1). it's a vertical line because the x-value remains the same while the y-value changes.
you have another vertical line that can be created between the points of (5,4) and (5,-1).
you have a horizontal line that can be created between the points of (-3,4) and (5,4). it's a horizontal line because the y-value remains the same while the x-value changes.
you have another horizontal line that can be created between the points of (-3,-1) and (5,-1)
your shaded region will be within the rectangle formed.
let's create the equations of the lines involved.
your 2 vertical lines will have the equations of x = -3, and x = 5.
your 2 horizontal lines will have the equations of y = 4, and y = -1.
your shaded region within the rectangle will be formed from the equations.
x > -3 and x < 5 which can be written as -3 < x < 5.
and:
y > -1 and y < 4 which can be written as -1 < y < 4.
x > -3 would be the area to the right of the line x = 3.
x < 5 would be the area to the left of the line x = 5
y > -1 would be the area above the line y = -1.
y < 4 would be the area below the line y = 4.
the area on the graph that is common to all these requirements is the area within the rectangle formed by the equations of these lines.
a picture of what your graph looks like is shown below:
|
|
|
| |