SOLUTION: Two points are chosen at random on a line segment whose length is a > 0. Find the probability that the 3 line segments thus formed can be the sides of a triangle.

Algebra ->  Inequalities -> SOLUTION: Two points are chosen at random on a line segment whose length is a > 0. Find the probability that the 3 line segments thus formed can be the sides of a triangle.      Log On


   

Question 397657: Two points are chosen at random on a line segment whose length is a > 0. Find the probability that the 3 line segments thus formed can be the sides of a triangle.
Found 2 solutions by robertb, Edwin McCravy:
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!


Let two of the segments have lengths x, y. Then the third segment must have length a - x - y. Use the triangle inequality on 3 different instances:
(i)x + y > a - x - y <==> x + y > a/2.
(ii) x +a - x - y > y <==> a/2 > y
(iii) Similarly , from y +a -x - y > x we get a/2 > x.

The initial conditions are x >0, y >0, and a - x -y >0, or a > x+y. In the Cartesian plane, this feasibility region is an (open) isosceles triangle with vertices at (0,0), (0, a), and (a,0). It has area 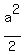a%5E2%2F2.
Incidentally, the region defined by the instances (i), (ii), and (iii) above is also an open isosceles triangle with vertices (a/2, 0), (a/2, a/2), and (0, a/2). This triangle has area %281%2F2%29%2A%28a%2F2%29%2A%28a%2F2%29+=+a%5E2%2F8.
Therefore the probability that the 3 line segments can be the sides of a triangle is %28a%5E2%2F8%29%2F%28a%5E2%2F2%29+=+2%2F8+=+1%2F4.

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!


The other tutor is right! Here's a bit more geometrical drawings:  

Suppose this is the line segment.

0------------x----------y------------a

Then the sides of the triangle are x, y-x, and a-y

The sum of any two sides must be greater than the third side.

So

x + (y-x) > a-y,    x + (a-y) > y-x,     (y-x) + (a-y) > x      y > x
x + y - x > a-y     x + a - y > y-x            y-x+a-y > x 
        y > a-y       2x - 2y > -a                -x+a > x   
       2y > a        -2x + 2y < a                    a > 2x
        y > a/2       2y - 2x < a                  a/2 > x   
                       2(y-x) < a                    x < a/2   
                          y-x < a%2F2          

We also know that y < a  and x > 0

So we have a system of inequalities:

system%28y%3Ca%2Cy%3Ea%2F2%2Cy-x%3Ca%2F2%2Cx%3E0%2C+x%3Ca%2F2%2C+y+%3E+x%29

We draw the boundary lines:




and find that the solution to the system of inequalities is the triangle
marked "SOLUTION".  It's area is 

A=expr%281%2F2%29%2Abase%2Aheight=expr%281%2F2%29%2Aexpr%28a%2F2%29%2Aexpr%28a%2F2%29%22%22=%22%22a%5E2%2F8

So the numerator of the probability is the area of that triangle, for
the coordinates of any point within that triangle will represent points
on the original line:


0------------x----------y------------a

that satisy the system of inequalities.

The denominator of the probability is the area of this triangle:


 
Because the coordinates of any point inside this triangle represents 
a pair of values for x and y that could have been picked on this line:

0------------x----------y------------a
 
The area of this triangle is expr%281%2F2%29%2Aa%2Aa=expr%281%2F2%29a%5E2

So the desired probability is  

%28AREA_OF_SMALLER_TRIANGLE%29%2F%28AREA_OF_LARGER_TRIANGLE%29

+%28%28a%5E2%29%2F8%29+%2F%28a%5E2%2F2%29+%22%22=%22%22expr%28a%5E2%2F8%29%22%22%2A%22%22expr%282%2Fa%5E2%29%22%22=%22%22expr%28cross%28a%5E2%29%2F8%29%22%22%2A%22%22expr%282%2Fcross%28a%5E2%29%29%22%22=%22%222%2F8%22%22=%22%221%2F4

Edwin