SOLUTION: Express the solution to the following inequality using interval notation. x2 + 10x + 24 ≥ 0

Algebra ->  Inequalities -> SOLUTION: Express the solution to the following inequality using interval notation. x2 + 10x + 24 ≥ 0       Log On


   

Question 356425: Express the solution to the following inequality using interval notation.
x2 + 10x + 24 ≥ 0
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2%2B10x%2B24%3E=0
%28x%2B6%29%28x%2B4%29%3E=0
Break up the number line into 3 regions using the critical points of the function.
Region 1:(-infinity,-6)
Region 2:(-6,-4)
Region 3:(-4,infinity)
.
.
.
For each region, choose a point in the region (not an endpoint).
Test the inequality.
If the ineqaulity is satisfied, the region is part of the solution region.
.
.
Region 1:x=-7
%28x%2B6%29%28x%2B4%29%3E=0
%28-7%2B6%29%28-7%2B4%29%3E0+
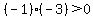
%28-1%29%28-3%29%3E0+
3%3E0+
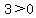
True, Region 1 is part of the solution region.
.
.
Region 2:x=-5
%28x%2B6%29%28x%2B4%29%3E=0
%28-5%2B6%29%28-5%2B4%29%3E0+
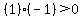
%281%29%28-1%29%3E0+
-1%3E0+
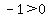
False, Region 2 is not part of the solution region.
.
.
.
Region 3:x=0
%280%2B6%29%280%2B4%29%3E=0
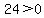
24%3E0+
True, Region 3 is part of the solution region.
.
.
.
Solution Region: (-infinity,-6) U (-4,infinity)
.
.
.
Graphical verification: Look for regions where the function is above the x-axis (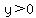y%3E0).
.
.
.