a)
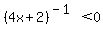
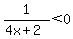
That is only true if the denominator is negative:

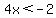
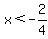
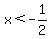 --------------------
--------------------
b)
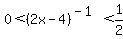
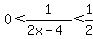 We must requre that the denominator
We must requre that the denominator  be positive,
so that we can multiple through by it without changing the order
of the inequality:
This requirement is
be positive,
so that we can multiple through by it without changing the order
of the inequality:
This requirement is
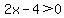
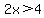

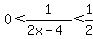
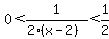 With this requirement, we multiply through by the LCD =
With this requirement, we multiply through by the LCD = 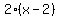
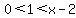
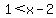
 which is the same as
which is the same as
 which is consistent with the requirement
which is consistent with the requirement  so the solution is
so the solution is
 Edwin
Edwin