Question 339897: How do i solve this polynomial inequality?
x^3+2x^2-3x>0.
Found 2 solutions by Fombitz, edjones:
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! First factor,
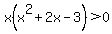
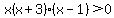
Now break up the number line into 4 regions base on the zeros of the polynomial,
Region 1: ( , )
Region 2: (, )
Region 3: (, )
Region 4: (,)
For each region choose a point in the region (not an endpoint).
Test the inequality.
If the inequality is satsfied, that region is part of the solution region.
.
.
.
Region 1:
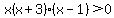
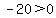
False, this region is not part of the solution region.
.
.
.
Region 2:
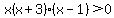
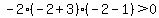
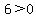
True, this region is part of the solution region.
.
.
.
Region 3:
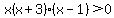
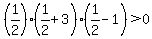
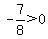
False, this region is not part of the solution region.
.
.
.
Region 4:
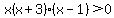
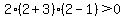
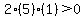
True, this region is part of the solution region.
.
.
.
Solution Region :(,) U (,)
.
.
.
Graphical verification: Look for the region where the function is above the x-axis.
.
.
.
Answer by edjones(8007)  (Show Source):
You can put this solution on YOUR website! x^3+2x^2-3x>0
first we find the zeros.
x(x^2+2x-3)=0
x(x+3)(x-1)=0
x=0, x=-3, x=1
.
Now we test on either side of the zeros.
x=-4 y=-20
x=-2 y=6
x=1/2 y=-.875
x=2 y=10
.
(-3, 0), (1, infinity) answer
.
Ed
.
|
|
|
