Question 300795: I am having a tough time solving this problem, any help would be much appreciated.
solve an inequality (x)/(x+20)>(2)/(x+8)
A. (-∞,-10) (-10,-8) (4,∞)
B. (-∞,-8) (4,∞)
C. (-10,-8)
D. (-20,-10) (-8,-4)
E. (-∞,-20) (-10,-8) (4,∞)
I came up with E but I'm not sure if the answer is correct.
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website!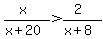 
Look at the inequality and determine when the left hand side equals the right hand side.
You can factor this quadratic,
Two solutions:  and 
In addition, because of the x terms in the denominator, add the additional points when the denominator goes to zero.
 and 
Set up a number line and break it up using these two points.
Region 1: ( , )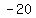
Region 2: ( , )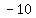
Region 3: ( , )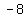
Region 4: ( , )
Region 5: (, )
Choose points in each region and check the inequality in that region to see if it's valid or not.
Region 1: Pick  .
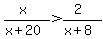
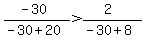
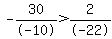
True, Region 1 is a valid region.
.
.
Region 2: Pick  .
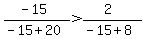
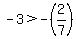
False, Region 2 is not a valid region.
.
.
Region 3: Pick x=-9.
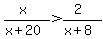
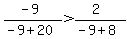
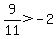
True, Region 3 is a valid region.
.
.
Region 4: Pick x=0.
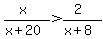
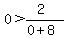
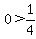
False, Region 4 is not a valid region.
.
.
Region 5: Pick x=10.
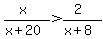
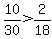
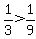
True, Region 5 is a valid region.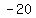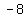
.
.
.
(,)U(,)U(,)
E is the correct answer.
|
|
|
