Here, we see two numbers are being multiplied together in the inequality ( and
and  ). And we know that the only way to multiply two numbers together and get a number less than 0 is to multiply a positive and a negative number together. (positive * positive = positive; and negative * negative = positive)
). And we know that the only way to multiply two numbers together and get a number less than 0 is to multiply a positive and a negative number together. (positive * positive = positive; and negative * negative = positive)
Thus, we know that 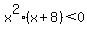 is true in either of the following situations:
is true in either of the following situations:
1. 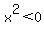 and
and 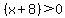
2. 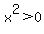 and
and 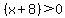
If you look at the first statement carefully, you may note that it can never be true. As previously stated, positive * positive = positive; and negative * negative = positive, so there is no way you can take any integer, square it, and get a negative number. This means, we only need to concern ourselves with the second situation, 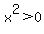 and
and 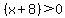 .
.
So, let's solve the two inequalities:
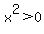
 (get the square root of both sides)
(get the square root of both sides)
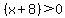
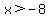
So, we get 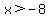 as our answer. (because all items > -8 are also > 0, so we use the more restrictive option as our final answer to ensure all possibilities work.)
as our answer. (because all items > -8 are also > 0, so we use the more restrictive option as our final answer to ensure all possibilities work.)
We can always double check our work. Let's take  , as that satisfies our answer condition. Plugging it into our original inequality:
, as that satisfies our answer condition. Plugging it into our original inequality:
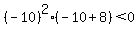

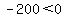 , which is a true statement.
, which is a true statement.