I'll do the first and last:
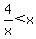 Get 0 on one side:
Get 0 on one side:
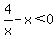
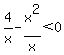
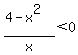
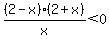 To find the critical values set numerator=0,
and denominator =0 and solve for x:
(2-x)(2+x)=0 gives 2 and -2 as critical values
x=0 gives 0 as a critical value.
So mark the critical values on a number line:
----------o-----o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
First select a test point in the region left
of -2. Choose x=-3. Substitute it in
To find the critical values set numerator=0,
and denominator =0 and solve for x:
(2-x)(2+x)=0 gives 2 and -2 as critical values
x=0 gives 0 as a critical value.
So mark the critical values on a number line:
----------o-----o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
First select a test point in the region left
of -2. Choose x=-3. Substitute it in
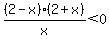
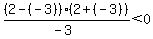
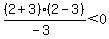
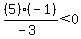

 That is false, so we do not shade the region
left of -2. So we still have the same
number line:
----------o-----o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
Next select a test point in the region between
-2 and 0. Choose x=-1. Substitute it in
That is false, so we do not shade the region
left of -2. So we still have the same
number line:
----------o-----o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
Next select a test point in the region between
-2 and 0. Choose x=-1. Substitute it in
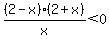
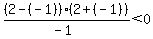
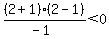
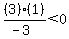
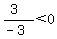
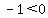 That is true, so we do shade the region between
-2 and 0. So now the number line is
----------o=====o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
Next select a test point in the region between
0 and 2. Choose x=1. Substitute it in
That is true, so we do shade the region between
-2 and 0. So now the number line is
----------o=====o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
Next select a test point in the region between
0 and 2. Choose x=1. Substitute it in
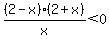
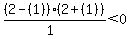
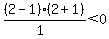

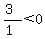
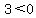 That is false, so we do not shade the region between
0 and 2. So the number line is still
----------o=====o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
finally select a test point in the region right
of 2. Choose x=3. Substitute it in
That is false, so we do not shade the region between
0 and 2. So the number line is still
----------o=====o-----o---------
-5 -4 -3 -2 -1 0 1 2 3 4 5
finally select a test point in the region right
of 2. Choose x=3. Substitute it in
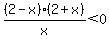
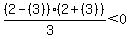
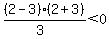
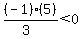
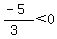
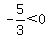 That is true, so we do shade the region
right of 2. So the final number line is:
----------o=====o-----o=========>
-5 -4 -3 -2 -1 0 1 2 3 4 5
Now we have to test the critical values
to see if they are solutions. But that's
easy because with strict inequality, none
of the critical values can be solutions.
In interval notation:
(-2,0) U (2,
That is true, so we do shade the region
right of 2. So the final number line is:
----------o=====o-----o=========>
-5 -4 -3 -2 -1 0 1 2 3 4 5
Now we have to test the critical values
to see if they are solutions. But that's
easy because with strict inequality, none
of the critical values can be solutions.
In interval notation:
(-2,0) U (2, )
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 Get 0 on one side
Get 0 on one side
 Get LCD of
Get LCD of 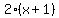





 To find the critical values set numerator=0,
and denominator =0 and solve for x:
(x-9)(x+2)=0 gives 9 and -2 as critical values
2(x+1)=0 gives -1 as a critical value.
So mark the critical values on a number line:
-------o--o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
---
First select a test point in the region left
of -2. Choose x=-3. Substitute it in
To find the critical values set numerator=0,
and denominator =0 and solve for x:
(x-9)(x+2)=0 gives 9 and -2 as critical values
2(x+1)=0 gives -1 as a critical value.
So mark the critical values on a number line:
-------o--o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
---
First select a test point in the region left
of -2. Choose x=-3. Substitute it in





 That is false, so we do not shade the region
left of -2. So we still have the same
number line:
-------o--o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Next select a test point in the region between
-2 and -1. Choose x=-1.5. Substitute it in
That is false, so we do not shade the region
left of -2. So we still have the same
number line:
-------o--o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Next select a test point in the region between
-2 and -1. Choose x=-1.5. Substitute it in





 That is true, so we do shade the region between
-2 and -1. So now the number line is
-------o==o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Next select a test point in the region between
-1 and 9. Choose x=0. Substitute it in
That is true, so we do shade the region between
-2 and -1. So now the number line is
-------o==o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Next select a test point in the region between
-1 and 9. Choose x=0. Substitute it in





 That is false, so we do not shade the region
between -1 and 9. So we still have the same
number line:
-------o==o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Finally select a test point in the region right
of 9. Choose x=10. Substitute it in
That is false, so we do not shade the region
between -1 and 9. So we still have the same
number line:
-------o==o-----------------------------o---------
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Finally select a test point in the region right
of 9. Choose x=10. Substitute it in




 That is true, so we do shade the region
right of 9. So the number line is now:
-------o==o-----------------------------o=========>
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Now we have to test the critical values
to see if they are solutions.
We test critical value -2
That is true, so we do shade the region
right of 9. So the number line is now:
-------o==o-----------------------------o=========>
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
Now we have to test the critical values
to see if they are solutions.
We test critical value -2





 That is true so we darken the circle at -2, like this:
-------@==o-----------------------------o=========>
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
We test critical value -1
That is true so we darken the circle at -2, like this:
-------@==o-----------------------------o=========>
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
We test critical value -1




 This undefined! So we do not darken the circle at -1,
but leave it open
Now we test critical point x=9
This undefined! So we do not darken the circle at -1,
but leave it open
Now we test critical point x=9





 That is true so we darken the circle at 9, like this:
-------@==o-----------------------------@=========>
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
The interval notation is:
[-2,-1) U [9,
That is true so we darken the circle at 9, like this:
-------@==o-----------------------------@=========>
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12
The interval notation is:
[-2,-1) U [9, )
Edwin
)
Edwin