|
Question 1208878: A man calculates that if he continues at the present speed, to drive the remaining 100km of his trip, he will arrive 30 minutes late. In order to arrive on time, he must travel at an average rate of 10 kph faster. What is his present speed?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x = the man's current speed in kph
y = time it takes to drive 100 km going at a speed of x kph
Let's consider the scenario where the man goes at his present speed.
distance = rate*time
d = r*t
100 km = (x kph)*(y hr)
100 = xy
y = 100/x
This will be used to substitute in later.
Now consider when he goes 10 kph faster, so his travel duration is 30 minutes = 30/60 = 0.5 hours less.
His old speed x is now x+10 kph.
The old time duration y is now y-0.5 hours.
So,
d = r*t
100 = (x+10)*(y-0.5)
100 = (x+10)*(100/x - 0.5) ........... replace y with 100/x
I'll let the student handle the scratch work from here.
Solving for x should give x = -50 and x = 40.
Ignore the negative solution because a negative speed makes no sense.
If the man travels at 40 kph, then he needs 100/40 = 2.5 hours to travel the 100 km.
If he travels instead at 40+10 = 50 kph, then he needs 100/50 = 2 hours, which is 0.5 hrs = 30 min early compared to the 2.5 hour figure. This confirms we have the correct present speed.
Answer: 40 kph
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A man calculates that if he continues at the present speed, to drive the remaining 100km
of his trip, he will arrive 30 minutes late. In order to arrive on time, he must travel
at an average rate of 10 kph faster. What is his present speed?
~~~~~~~~~~~~~~~~~~
Let v be the man's present speed, in kilometers per hour.
Then the other, hypothetical speed is (v+10) km/h.
The time to drive 100 km at the speed v km/h is 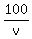 hours.
The time to drive 100 km at the speed (v+10) km/h is hours.
The time to drive 100 km at the speed (v+10) km/h is 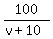 hours.
The problem says that time hours.
The problem says that time 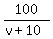 is 30 minutes, or 1/2 of an hour less than time is 30 minutes, or 1/2 of an hour less than time 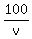 .
So, we write this time equation .
So, we write this time equation
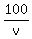 - - 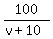 = =  of an hour.
At this point, the setup is complete.
To solve this equation, multiply its terms by 2v*(v+10) in both sides.
You will get
100*2*(v+10) - 100*2*v = v*(v+10),
200v + 2000 - 200v = v^2 + 10v
v^2 + 10v - 2000 = 0.
Factor left side
(v+50)*(v-40) = 0.
This equation has two roots, v= -50 and v= 40.
Since v should be positive, due to its meaning, we accept the positive root v= 40 km/h
and deny the negative root.
So, the ANSWER to the problem is that the present speed of driving is 40 km/h.
CHECK. Driving time at the present speed is of an hour.
At this point, the setup is complete.
To solve this equation, multiply its terms by 2v*(v+10) in both sides.
You will get
100*2*(v+10) - 100*2*v = v*(v+10),
200v + 2000 - 200v = v^2 + 10v
v^2 + 10v - 2000 = 0.
Factor left side
(v+50)*(v-40) = 0.
This equation has two roots, v= -50 and v= 40.
Since v should be positive, due to its meaning, we accept the positive root v= 40 km/h
and deny the negative root.
So, the ANSWER to the problem is that the present speed of driving is 40 km/h.
CHECK. Driving time at the present speed is 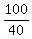 = 2 = 2 hours.
Driving time at the speed of 40+10 = 50 km/h is hours.
Driving time at the speed of 40+10 = 50 km/h is  = 2 hours.
The difference of the two driving times is 1/2 of an hour, or precisely 30 minute,
which confirms that the answer is correct. = 2 hours.
The difference of the two driving times is 1/2 of an hour, or precisely 30 minute,
which confirms that the answer is correct.
Solved completely.
This solution method (using time equation) is a standard approach for solving similar problems.
|
|
|
| |