Question 1203082: Solve for x, assuming a, b and c are negative constants.
(a) ax + b < c
(b) (ax +b)/c < or = b
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve for x, assuming a, b and c are negative constants.
(a) ax + b < c
(b) (ax +b)/c <= b
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(a) Step by step
Starting inequality to solve is
ax + b < c.
Subtract "b" from both side. You will get
ax < c - b.
Divide both sides by "a". Since "a" is negative (given), change the sign
of the inequality to the opposite one. You will get
x > 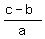 . ANSWER
(b) Step by step
Starting inequality is . ANSWER
(b) Step by step
Starting inequality is
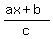 <= b.
Multiply both sides by "c". Since "c" is negative number, change the sign of the inequality
to the opposite one. You will get
ax + b >= bc.
Next, subtract "b" from both sides of the last inequality. You will get
ax >= bc - b.
Now divide both sides by "a". Since "a" is negative number, change the sign of the inequality
to the opposite one. You will get
x <= <= b.
Multiply both sides by "c". Since "c" is negative number, change the sign of the inequality
to the opposite one. You will get
ax + b >= bc.
Next, subtract "b" from both sides of the last inequality. You will get
ax >= bc - b.
Now divide both sides by "a". Since "a" is negative number, change the sign of the inequality
to the opposite one. You will get
x <= 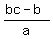 = = 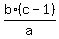 .
Answer. x <= .
Answer. x <= 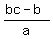 , or, equivalently, x <= , or, equivalently, x <= 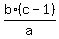 . .
Solved in full, with explanations.
------------------
In writing Math, do not use this mixed combination of words and symbols " < or = ",
as it was in your post originally (before I fixed it).
Instead, use the symbol " <= ".
|
|
|