|
Question 1199000: Solve for x the inequality equation (x+9)/(x+1) -2 > 0
The correct answer is one of the following. Which one is correct?
A) -1 < x < 7
B) x > 7
C) -1 < x < 8
D) x > 8
Found 2 solutions by greenestamps, math_tutor2020:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!
Given the answer choices, by far the quickest path to the answer is to see which one works. From the given answer choices, the x values -1, 7, and 8 need to be the endpoints of the solution interval(s) -- which means the value of the expression is either 0 or undefined at those values.
The expression is undefined at x=-1 and 0 at x=7; it is neither 0 nor undefined at x=8. Since the inequality is a strict inequality (endpoints of the intervals not included), the solution set is either (-1,7) or (-infinity,-1) U (7,infinity). But that second possibility is not one of the answer choices, so
ANSWER: A) (-1,7)
But surely the intended purpose of the problem was for you to learn how to get that answer....
Keep everything on one side of the inequality, with "0" on the other side; and combine the terms on the left with a common denominator so the expression is a rational function.
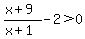
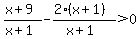
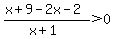
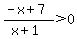
That rational function is equal to 0 at x = 7 and is undefined at x = -1, so those are endpoints of the interval(s) of the solution set. And evaluating the expression at x = 0 shows the inequality is satisfied, so the solution set is (-1,7).
Answer by math_tutor2020(3816)  (Show Source):
|
|
|
| |
