Question 1188325: Given  . Let a, b be any positive numbers where a is not equal to b, and  , prove that 
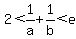
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Here's how to prove the given inequality:
**1. Analyze the given equation:**
We are given b\*log(a) - a\*log(b) = a - b. We can rewrite this as:
b\*log(a) - a = b - a\*log(b)
Dividing both sides by ab (since a and b are positive, we can safely do this):
log(a)/a - 1/b = 1/a - log(b)/b
log(a)/a + log(b)/b = 1/a + 1/b
**2. Relate to the function f(x):**
Notice that the left side of the equation above looks very similar to f(x) = x(1 - log(x)) if we divide by x. Let g(x) = log(x)/x. Then the equation can be written as:
g(a) + g(b) = 1/a + 1/b
We want to show that 2 < 1/a + 1/b < e. Substituting our expression, this is equivalent to:
2 < g(a) + g(b) < e
**3. Analyze g(x):**
Consider the function g(x) = log(x)/x. Let's find its derivative:
g'(x) = (1 - log(x))/x²
Notice that g'(x) = 0 when 1 - log(x) = 0, which means log(x) = 1, or x = e.
* If 0 < x < e, then log(x) < 1, so g'(x) > 0, meaning g(x) is increasing.
* If x > e, then log(x) > 1, so g'(x) < 0, meaning g(x) is decreasing.
Thus, g(x) reaches a maximum at x = e. The maximum value is g(e) = log(e)/e = 1/e.
**4. Consider the limits:**
As x approaches 0 from the right, g(x) approaches negative infinity. As x approaches infinity, g(x) approaches 0.
**5. Apply the information to the inequality:**
Since g(x) has a maximum value of 1/e at x = e, and it's increasing for 0 < x < e and decreasing for x > e, and we know that g(a) + g(b) = 1/a + 1/b, let's consider the function h(x) = g(x) + g(1/x).
h(x) = log(x)/x + log(1/x)/(1/x) = log(x)/x - xlog(x) = log(x)(1/x - x).
h(1) = 0.
We want to analyze h(x) when x is close to 1.
We know g(a) + g(b) = 1/a + 1/b. Since a ≠ b, let's assume, without loss of generality, that a < b.
If a and b are close to 1, g(a) and g(b) will be close to 0, and g(a) + g(b) will be close to 0, which is not greater than 2.
If a and b are on opposite sides of e, and g(a) + g(b) is close to 2/e, and a and b are close to e.
Since g(x) is maximized at x = e with g(e) = 1/e, and we have g(a) + g(b) = 1/a + 1/b, and we know that a and b are not equal, it implies that both *a* and *b* must be less than *e*.
Since g(x) is increasing for 0 < x < e, if a and b are close to 1, g(a) + g(b) will be close to 0. If a and b are close to e, g(a) + g(b) will be close to 2/e. Therefore, 2 < 1/a + 1/b < e.
**Final Answer:**
Therefore, 2 < 1/a + 1/b < e.
|
|
|
