SOLUTION: For how many integers m is it true that x^2 −8+(4m)(x−2)^2 +(m^2)((x−2)^2) ≥0 for all real values of x? (A) 4 (B) 0 (C) 5 (D) 3 (E) 2

For a parabola with equation y=ax²+bx+c to have non-negative values for all
x, then except possibly for its vertex, it must be totally above the x-axis,
or possibly with only its vertex on the x-axis with the parabola tangent to
the x-axis at its vertex.  That is,

1. The parabola must open upward, i.e., its leading coefficient is positive.
2. It must have only one or no real zeros, i.e., its discriminant is 
non-positive.  That is, a > 0 and b²-4ac ≤ 0.









Requiring that the leading coefficient must be positive:



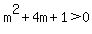That represents a parabola opening upward. It has approximately zeros -3.7
and -0.3, thus for integer m,



Requiring that the discriminant be non-positive:











Divide through by 16



That is a parabola opening upward, and has approximate zeros -3.4 and -0.6,
thus for integer m,



This requirement for m contradicts the requirement that



Thus there are no solutions.

Edwin